| |
Artículo Original
Aplicación de la descomposición de valores singulares a un sistema de recuperación de información
Singular value decomposition applied to information retrieval system
Osvaldo SPOSITTO (1), Viviana LEDESMA (2), Gastón PROCOPIO (3)
(1) Universidad Nacional de La Matanza
spositto@unlam.edu.ar
(2) Universidad Nacional de La Matanza
vledesma@unlam.edu.ar
(3) Universidad Nacional de La Matanza
gprocopio@unlam.edu.ar
Resumen:
Este artículo se realiza en el marco de una investigación que tiene por objetivo optimizar un Sistema de Recuperación de Información, de desarrollo propio, mediante implementar y evaluar distintos algoritmos secuenciales y paralelos para resolver eficientemente la Descomposición de Valores Singulares. Dicho proceso comienza con la reducción de la matriz inicial a la forma bidiagonal. Estudios demuestran que la bidiagonalización puede consumir más del 70% del tiempo total del proceso. Por ello, como trabajo preliminar se han estudiado distintos métodos de bidiagonalización y se ha implementado un algoritmo basado en las transformaciones de Householder. El mismo se ha planteado con la suficiente flexibilidad como para ser adaptado fácilmente a otros algoritmos alternativos con el fin de realizar futuras implementaciones en arquitecturas paralelas, en particular las basadas en unidades de procesamiento gráfico.
Palabras Clave: Descomposición de Valores Singulares, Bidiagonalización, Sistemas de Recuperación de Información
Abstract:
This article is written in the context of an investigation whose objective is to optimize an information retrieval system in-house developed. It is done through the implementation and evaluation of different sequential and parallel algorithms to efficiently resolve the singular value decomposition. This process begins with the bidiagonal reduction of the initial matrix. Studies show that the bidiagonalization process can consume more than 70% of the overall time. Consequently, as groundwork, different bidiagonalization methods have been studied and one specific algorithm based on Householder transformations has been implemented. The latter has been set out with enough flexibility to be easily adapted to alternative algorithms in order to make future implementations in parallel architectures, particularly those based on graphic processing units.
Key Words: Singular Value Decomposition, Bidiagonalization, Retrieval Information System
Colaboradores: Fabio QUINTANA, Victoria SAIZAR, Alexis VAINBERG
I. CONTEXTO
Este artículo se enmarca en una línea de investigación, relacionada a los Sistemas de Recuperación de Información (SRI) realizada por investigadores del Departamento de Ingeniería e Investigaciones Tecnológicas de la Universidad Nacional de La Matanza. Particularmente se asocia al proyecto PROINCE, código C225, Resolución Eficiente de la Descomposición en Valores Singulares en una Arquitectura Híbrida y su Posterior Inserción en un Sistema de Recuperación de Información, con vigencia 2019-2020.
II. INTRODUCCIÓN
Desde un punto de vista práctico la Descomposición de Valores Singulares (DVS) tiene diferentes aplicaciones, compresión de imágenes digitales, reconocimiento facial, sistemas de recomendación, la indexación semántica latente (LSI, por sus siglas en inglés), entre otros [1].
Dado que el contexto de esta investigación se relaciona a un SRI desarrollado por el propio equipo, la LSI resulta de particular interés. Se trata de un método para la búsqueda de información en documentos a través de la indexación de términos [2]. Con la LSI se pretende la resolución de perturbaciones en la recuperación de información debido a problemas de sinonimia y polisemia o equivocidad del habla corriente. Por ejemplo, si se desea buscar la palabra “estación”, la cual tiene múltiples significados (polisemia) una búsqueda literal de la palabra produciría muchos resultados posibles (estación de tren, estación del año, etc.). Si lo que se desea buscar es “estación del año”, podrían interesar resultados de palabras distintas, pero con un significado igual o similar, por ejemplo “temporada”, “época” y así por el estilo (sinonimia). La LSI permite la búsqueda por conceptos o definiciones (en contraposición a la búsqueda literal).
Con tal objetivo se aplican algoritmos matemáticos especializados, que como resultado simulan el análisis que realizaría una persona. Una técnica ampliamente utilizada a tal fin es la DVS, luego la recuperación se realiza utilizando como punto de partida los valores singulares y vectores obtenidos a partir de la aplicación de dicha técnica [3].
Mediante este proyecto se pretende optimizar la resolución de la DVS, en especial mediante implementar algoritmos para resolver la primera fase de este proceso, la bidiagonalización. El resultado final de este proyecto se orienta hacia algoritmos que puedan ser implementados en plataformas paralelas y, en particular aprovechando la capacidad de las unidades de procesamiento gráfico (GPU, por sus siglas en inglés). En principio fue necesario evaluar distintos métodos de bidiagonalización y, a modo inicial, se implementó un algoritmo genérico, secuencial, que sirvió para evidenciar el funcionamiento interno del proceso.
III. MÉTODOS
La metodología utilizada para cumplir con los objetivos de este proyecto se llevará adelante realizando los siguientes pasos:
• Revisión en la literatura sobre los fundamentos matemáticos de la DVS y sus posibles variantes.
• Estudio de las tecnologías existentes para la implementación de la programación en paralelo que utiliza GPU.
• Análisis de las librerías paralelas: CUDA (Compute Unified Device Architecture) y CuBlas (CUDA Basic Linear Algebra Subprograms) para guiar en la instalación, introducción a la arquitectura, desarrollo y ejecución de programas que utilicen la tecnología BLAS (Basic Linear Algebra Subprograms) y LAPACK (Linear Algebra PACKage), como herramienta de apoyo para Computación de Altas Prestaciones.
• Desarrollo de librerías propias en lenguaje de programación C#.
IV. RESULTADOS Y OBJETIVOS
En esta etapa preliminar del proyecto se ha implementado un algoritmo en el lenguaje de programación C# para la bidiagonalización basada en transformaciones de Householder. Si bien existía la posibilidad de utilizar la biblioteca LAPACK , la documentación y las rutinas utilizadas en este paquete resultan más difíciles de entender y requieren más tiempo para dominarse. En cambio, el disponer del código en C# ofrece como ventaja, por una parte, permitir la comprensión de cada etapa interna del proceso, y por otra sienta las bases para que este código posteriormente pueda ser adaptado a diferentes algoritmos de bidiagonalización, e implementarlos en otras arquitecturas paralelas, en particular aquellas basadas en GPU, a fin de analizar su eficiencia.
Los próximos objetivos por cumplir para este proyecto son los siguientes:
• Implementar los algoritmos alternativos propuestos por Ralha y por Barlow, en una arquitectura basada en CPU.
• Adaptar los mismos algoritmos para ser implementados en una arquitectura basada en GPU.
• Realizar un estudio comparativo en cuanto al rendimiento al bidiagonalizar matrices de variados tamaños cuando se utilizan distintas implementaciones variando la arquitectura. Determinando que algoritmo e implementación resulta más eficiente.
• Calcular la DVS utilizando el algoritmo identificado en el punto anterior, y finalmente implementarlo en el SRI desarrollado por el equipo.
V. DVS APLICADO A LA RECUPERACIÓN DE INFORMACIÓN
Se han ideado diferentes modelos basados en distintos paradigmas para representar tanto documentos como consultas en SRI y comparar la similitud de esas representaciones [3]. Entre estos se encuentran el modelo booleano, el modelo vectorial y el modelo probabilístico, denominados clásicos. El trabajo de investigación en curso cuya etapa inicial se presenta en este artículo se enmarca en una variante del método de RI vectorial, la LSI [2].
Con la LSI se define un espacio semántico donde los términos y los documentos altamente relacionados son colocados unos cerca de otros, reflejando los patrones de asociación entre los datos más importantes e ignorando los menos importantes, es decir los que tienen menor influencia al momento de la recuperación.
La técnica estadística particular que se aplica es la DVS de una matriz [2], [4]. Esta es una técnica ampliamente usada para descomponer una matriz en varias matrices que exhiben las propiedades más importantes de la matriz original. Así, una matriz A de tamaño t × d descompuesta con DVS (ver Fig. 1) produce tres matrices de la forma:
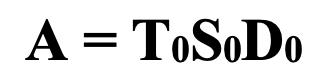
1. http://www.netlib.org/lapack/
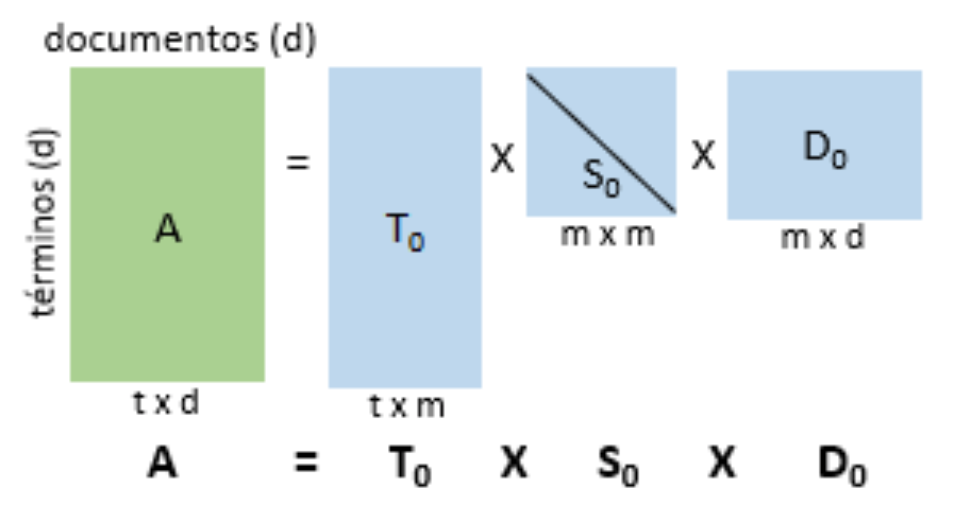 Fig. 1. Reducción de las dimensiones en DVS. Fuente [2] Fig. 1. Reducción de las dimensiones en DVS. Fuente [2]
T0 y D0 tienen columnas ortonormales (ortogonales y de tamaño uno) y son las matrices izquierda y derecha, respectivamente, de vectores singulares y S0 es una matriz diagonal compuesta de los valores singulares de A.
La importancia de obtener modelos de orden reducido tiene que ver con que simplifican la comprensión del sistema, reducen el coste computacional en los problemas de simulación, implican menor esfuerzo computacional en el diseño de controladores numéricamente más eficientes y se obtienen leyes de control más simples [5].
Por ello es necesario buscar modelos matemáticos más simples que aproximen al máximo el comportamiento del sistema original. Este modelo, que poseerá menor número de estados que el sistema original, se denomina modelo reducido o modelo de orden reducido y al procedimiento utilizado para conseguirlo reducción de modelo.
Existen dos tipos principales de algoritmos utilizados en el cálculo computacional de la DVS de una matriz real: el método unilateral de Jacobi y algoritmos basados en bidiagonalización [6]. Este trabajo se enfoca en los algoritmos basados en bidiagonalización, los cuales aplican transformaciones ortogonales con el fin de obtener una forma bidiagonal para luego conseguir la DVS de la matriz bidiagonal.
VI. ALGORITMOS PARA BIDIAGONALIZACIÓN
La reducción bidiagonal de una matriz densa general se usa muy frecuentemente como un paso previo para calcular la DVS [7], [8].
A partir de la revisión en la literatura se descubrió que existen distintos métodos para la bidiagonalización de una matriz, los más tradicionales utilizan las transformaciones de Householder por la izquierda y por la derecha de la matriz [6], [9], [10]. Estudios realizados demuestran que estos presentan dos desventajas: cuando las matrices son de grandes dimensiones requieren tiempos de computación elevados y además repercuten negativamente en los costos de comunicación de una implementación paralela del algoritmo en sistemas de memoria distribuida [11], [12]. De hecho, según Ltaief [8], el número total de operaciones para dicho algoritmo sea 8/3 n3, siendo n previsible de varios miles.
Con el énfasis puesto en dar una solución a estos problemas se han realizado diversos trabajos, entre estos se encuentran la propuesta de Ralha [13], mejorada más adelante por Barlow [14], orientada a conseguir un método más sencillo de paralelizar que los métodos tradicionales. En esta propuesta la bidiagonalización es unilateral, las transformaciones de Householder son aplicadas solamente por el lado derecho de la matriz.
Posteriormente Da Silva Sanches de Campos [12] presenta una mejora al método de Barlow con el objetivo de reducir el número de comunicaciones necesarias para una implementación paralela destinada a sistemas de memoria distribuida.
El método de bidiagonalización suele ser altamente paralelizable debido a las operaciones que utiliza en el proceso [15]. Vale mencionar que la correcta ejecución de algoritmos paralelos depende fuertemente de que los tamaños de las matrices se adapten a las capacidades de la máquina donde estos se ejecutan, por lo que, en matrices de alta dimensionalidad, surgen problemas como el espacio en la memoria, la correctitud del algoritmo y el incremento en los tiempos de ejecución.
Con lo anterior presente, se han realizado numerosos trabajos que incluyen estudios comparativos en cuanto al rendimiento al bidiagonalizar matrices de variados tamaños cuando se utilizan distintas implementaciones variando la arquitectura. Entre estos, se han contrastado implementaciones secuenciales y paralelas sobre una arquitectura homogénea basada en CPU [12]; se han experimentado algoritmos en mosaico con distinta cantidad de nodos multinúcleo de un sistema de memoria compartida distribuida en paralelo [8], [16]. Otros han buscado aprovechar la capacidad que ofrecen las Unidades de Procesamiento Gráfico (GPU) y experimentaron su uso aplicando algoritmos en arquitecturas tanto homogéneas [17], [18] como también heterogéneas en las que se combinan el uso de CPU con GPU [19].
En este proyecto se decide poner especial interés en los algoritmos alternativos de bidiagonalización propuestos por Ralha y Barlow [13], [14], dado que están pensados para soportar el paralelismo, ya que la proyección a futuro es realizar la paralelización de los mismos a partir de una arquitectura basada en GPU.
A modo preliminar se decidió construir un algoritmo genérico en el lenguaje C# para el cálculo de la bidiagonalización basado en las transformaciones de Householder [8], el cual servirá de base tanto para comprender el proceso en sí mismo, como también, para tomarlo como referencia en el diseño e implementación de los otros dos algoritmos mencionados antes. El algoritmo 1 toma como entrada una matriz densa A y da como salida la descomposición bidiagonal superior. Los reflectores uj y vj pueden almacenarse en las partes inferior y superior de A, respectivamente. La mayor parte del cálculo se encuentra en la línea 5 y en la línea 10 en la que los reflectores se aplican a la matriz A desde la izquierda y luego desde la derecha, respectivamente. Se necesitan 4 flops para llevar a cero un elemento de la matriz, lo que hace que el número total de operaciones para dicho algoritmo sea 8/3 n3.

VI. CONCLUSIONES
SParte del trabajo de este proyecto de investigación tiene que ver con optimizar el proceso de bidiagonalización implementando para ello un algoritmo en una arquitectura híbrida basada en GPU. A modo preliminar, con el objetivo de lograr una mayor comprensión del proceso, se ha desarrollado un algoritmo en el lenguaje C# para la reducción de una matriz a su forma bidiagonal vía reflectores de Householder. El principal aporte de esta primera etapa tiene que ver con que dicho algoritmo ofrece evidencia de las funciones internas del proceso de bidiagonalización, algo que resulta engorroso de comprender cuando se utilizan rutinas de la biblioteca LAPACK. Vale aclarar que el algoritmo solo se ha realizado a modo demostrativo, aunque los resultados coinciden con los obtenidos al usar la biblioteca LAPACK, aun debe ser optimizado para futuras implementaciones en arquitecturas paralelas. Sin embargo, este ha sido desarrollado con la suficiente flexibilidad para ser adaptado a futuro al momento de evaluar y comparar otras alternativas.
VII. REFERENCIAS Y BIBLIOGRAFÍA
A. Referencias bibliográficas:
[1] M. Mamani Roque. “Descomposición en Valores Singulares y Análisis Semántico Latente”. Tesis de Maestría. Universidad Politécnica de Valencia, España, 2018.
[2] S. Deerwester, S. Dumais, G. Furnas, T. Landauer & R. Harshman. “Indexing by latent semantic analysis”. Journal of the American Society for Information Science. 41(6):391–407. 1990.
[3] Tolosa G. & Bordignon, F. “Introducción a la Recuperación de Información: Conceptos, modelos y algoritmos básicos”. Universidad Nacional de Luján, Argentina, 2008. Recuperado el 01/08/2019 de: http://eprints.rclis.org/12243/1/Introduccion-RI-v9f.pdf
[4] Berry, M., Dumais, S. & O’Brien, G. “Using Linear Algebra For Intelligent Information Retrieval”. Society for Industrial and Applied Mathematics, Review 37(4): 573-595. Philadelphia, USA, 1995.
[5] L. Fortuna, G. Nunnari & A. Gallo. “Model order reduction techniques with applications in electrical engineering”. Springer-Verlag, 1992.
[6] J. Demmel, M. Gu, S. Eisenstat, et al. “Computing the Singular Value Descomposition with Hight Relative Accuracy”. Linear Algebra and its Application, 299, 21-80, 1999.
[7] Golub, G. & Van Loan, C. Matrix Computation. John Hopkins Studies in the Mathematical Sciences. Johns Hopkins University Press, Third Edition, 1996.
[8] Ltaief, H., Kurzak, J. & Dongarra, J. “Parallel Two-Sided Matrix Reduction to Band Bidiagonal Form on Multicore Architectures”. IEEE Transactions on Parallel and Distributed Systems, 21(4): 417 – 423, 2010.
[9] G. Golub & C. Reinsch. “Singular Value Decomposition and Least Squares Solutions”, Handbook Series Linear Algebra, 14: 403-420, 1970.
[10] T. Chan. “An Improved Algorithm for Computing the Singular Value Decomposition”. ACM Transactions on Mathematical Software, 8(1): 72-83, 1982.
[11] Sangwine, S. & Le Bihan, N. “Quaternion Singular Value Decomposition based on Bidiagonalization to a Real Matrix using Quaternion Householder Transformations” Applied Mathematics and Computation, ELSEVIER, 182(1): 727-738, 2006.
[12] Da Silva Sanches de Campos, C. “Algoritmos de Altas Prestaciones para el Cálculo de la Descomposición en Valores Singulares y su Aplicación a la Reducción de Modelos de Sistemas Lineales de Control”. Tesis Doctoral. Departamento de Sistemas Informáticos y Computación, Universidad Politécnica de Valencia, España, 2014.
[13] Ralha, R. “One-sided reduction to bidiagonal form”. Linear Algebra and Its Applications, ELSEVIER, 358(1-3): 219-238, 2003.
[14] Barlow, J., Bosner, N., Drmač, Z. “A new stable bidiagonal reduction algorithm”. Linear Algebra and Its Applications, ELSEVIER, 397: 35-84, 2005.
[15] Guerrero López, D. “Algoritmos Paralelos para la Reducción de Sistemas Lineales de Control Estables”. Tesis doctoral. Departamento de Sistemas Informáticos y Computación, Universidad Politécnica de Valencia, España, 2015.
[16] Faverge M., Langou, J., Robert, Y. & Dongarra, J. “Bidiagonalization and R-Bidiagonalization: Parallel Tiled Algorithms, Critical Paths and Distributed-Memory Implementation”. IEEE Transactions on Parallel and Distributed Processing Symposium, 668 - 677, 2017.
[17] Lahabar, S. & Narayanan, P. “Singular Value Decomposition on GPU using CUDA”. IEEE International Symposium on Parallel & Distributed Processing, 1-10, 2009.
[18] Dong, T., Haidar, A., Tomov, S. & Dongarra, J. “Optimizing the SVD Bidiagonalization Process for a Batch of Small Matrices”. Linear Algebra and Its Applications, ELSEVIER, 108: 1008-1018, 2017.
[19] Hernández Cortés, J. “Implementación paralela y heterogénea de la transformación de Householder y sus aplicaciones”.Tesis de Maestría. Departamento de Computación, Unidad Zacatenco, México, 2017.
B. Bibliografía:
A. Howard, C. Rorres. Elementary Linear Algebra. Wiley. USA, 11th edition, 2017.
Recibido: 2019-12-27
Aprobado: 2019-01-23
Datos de edición: Vol.4 - Nro.2 - Art.5
Fecha de edición: 2020-01-31
Hipervínculo Permanente: http://www.reddi.unlam.edu.ar
| |