| |
Artículo Original
Evaluando el aprendizaje del concepto de derivada en alumnos de Ingeniería de La Universidad Nacional de La Matanza
Assessing learning derivative’s concept to engineering students of The National University of The Matanza
Adriana FAVIERI (1), Betina WILLINER (2), Roxana SCORZO (3)
(1) Universidad Nacional de La Matanza
afavieri@unlam.edu.ar
(2) Universidad Nacional de La Matanza
bwilliner@unlam.edu.ar
(3) Universidad Nacional de La Matanza
rscorzo@unlam.edu.ar
Resumen:
En este artículo se presentan resultados de las acciones de la primera parte de una investigación realizada con alumnos de Análisis Matemático I, del Departamento de Ingeniería e Investigaciones Tecnológicas, de la Universidad Nacional de La Matanza con el fin de evaluar el aprendizaje del concepto de derivada y sus aplicaciones. Se diseñaron tareas en las que se refleja dicho concepto en tres contextos diferentes: uno geométrico, y dos físicos, uno vinculado a la velocidad de un móvil y el otro con el volumen de un gas. Éstas tienen por finalidad que el alumno aplique y reconozca el concepto de derivada en distintas situaciones. Se muestran los resultados obtenidos sobre el aprendizaje de los alumnos en dichas tareas. La conclusión principal es que estos resultados constituyen un punto de partida para la elaboración de un recurso didáctico utilizando la aplicación GeoGebra que favorezca el aprendizaje del concepto de derivada.
Palabras Clave: aplicaciones de derivada, contexto geométrico, contexto físico
Abstract:
This article shows the results of the actions carried out in the first part of an investigation performed at National University of La Matanza, Department of Engineering and Technological Research. The goal of these actions is to assess students' learning of the derivative's concept and its applications. Designed tasks reflect the concept in three different contexts: one geometric, and two physical, one linked to mobile’s speed and the other to gas’ volume. In these tasks students can apply and recognize the derivative's concept in different situations. The students' learning results are exhibited. These results constitute a starting point for a didactic resource’s design using the GeoGebra app that promotes the learning of the derivative's concept.
Key Words: derivative applications, geometric context, physical context
I. Contexto
Este trabajo surge en el proyecto presentado en el Departamento de Ingeniería e Investigaciones Tecnológicas (DIIT), de la Universidad Nacional de La Matanza (UNLaM), en el marco del programa de investigación que tiene como objetivo promover mejoras en el sistema educativo de las carreras de Ingeniería y Arquitectura, PROINCE, código C212, Dispositivo móvil como recurso didáctico en la enseñanza de Análisis Matemático, con vigencia 2018-2019. El objetivo principal del mismo es desarrollar un recurso didáctico utilizando la aplicación GeoGebra para mejorar el proceso de enseñanza aprendizaje del concepto de derivada. Con el fin de establecer la eficacia de dicho recurso didáctico fue preciso evaluar el aprendizaje de dicho concepto al inicio del proyecto. De esta manera asentamos las bases para el diseño del recurso y la evaluación del concepto al finalizar la investigación.
II. Introducción
Es preciso que el futuro ingeniero adquiera conocimientos sobre el Cálculo diferencial e integral debido a que muchas aplicaciones físicas e ingenieriles utilizan sus conceptos para ser resueltas. El Cálculo diferencial se centra en el estudio de las variaciones de variables, en cómo cambia la variable dependiente con respecto a variaciones de la variable independiente. Surgen así dos conceptos fundamentales: el de razón de cambio media y el de razón de cambio instantánea.
Tiene numerosas aplicaciones, por ejemplo, en Matemática permite calcular los puntos máximos y mínimos de curvas. En Física, el cálculo de la velocidad y aceleración instantánea. En Química, posibilita el estudio de fenómenos evolutivos asociados con el tiempo, como la velocidad de flujos [1],[2],[3],[4].
III. Métodos
Se trata de una investigación de tipo exploratoria con una fase indagatoria y una segunda de desarrollo. En el presente artículo se muestra la parte de la fase indagatoria que consiste en evaluar los niveles iniciales de aprendizaje de los estudiantes acerca del concepto de derivada.
A. Sobre resolución de problemas y/o tareas
El CONFEDI considera la competencia resolución de problemas como parte importante de la formación del ingeniero. Sostiene que, en distintas investigaciones realizadas desde la psicología cognitiva, se identifican los mismos procesos en la resolución de problemas: representación del problema (comprensión de este); transferencia del conocimiento (activación y aplicación de conocimientos previos en la elaboración de un plan para resolverlo); evaluación de la solución hallada y comunicación de los resultados [5].
Pueden encontrarse diversos tipos de actividades en relación con la resolución de problemas en la enseñanza de la Matemática. Entre ellas están los llamados problemas de traducción simple o compleja, que son aquellos formulados en un contexto concreto y cuya resolución supone una traducción del enunciado, oral o escrito, a una expresión matemática. En el enunciado del problema aparece toda la información necesaria para la resolución y suele indicar, implícitamente, la estrategia a seguir. A través de ellos se intenta fortificar la comprensión de los conceptos matemáticos y de las habilidades computacionales de los alumnos y lograr que estos sean capaces de traducir situaciones del mundo real a expresiones matemáticas [6].
B. Precisando conceptos
Función: “Una función es una relación entre dos variables en la cual a cada valor de la primera (independiente) le corresponde un único valor de la segunda (dependiente)” [7]. Simbólicamente se escribe: y=f(x), siendo x la variable independiente e y la dependiente.
Incrementos de las variables
Incremento de la variable independiente: Se llama así a la diferencia entre el valor final y el inicial. Se utiliza el símbolo Δx=xf- xi. Incremento de la variable dependiente: se llama así a la diferencia entre la imagen del valor final y la del valor inicial. Se utiliza el símbolo Δy=f(xf)-f( xi). (Gráfico 01)
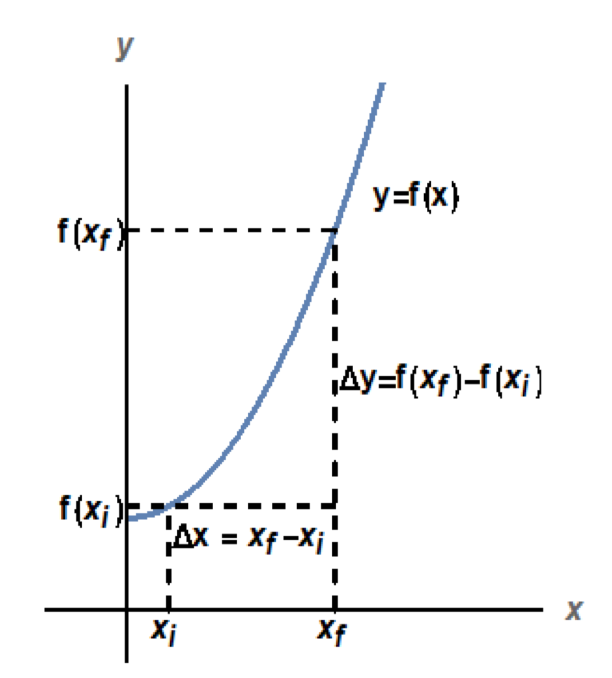Gráfico 01: Incrementos Fuente: Elaboración propia
Razón de cambio promedio (RCP): es el cociente entre el incremento de la variable dependiente y el de la variable independiente. Simbólicamente: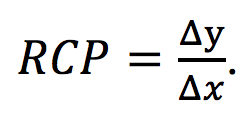 
Razón de cambio instantánea (RCI): es el límite de la RCP cuando Δx tiende a cero. La RCI es la derivada de la función en el punto inicial.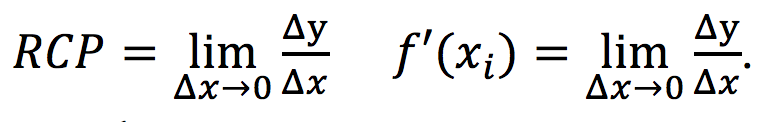 
Recta secante: es la recta que corta a una curva en dos puntos. En este caso en particular la recta que pasa por los puntos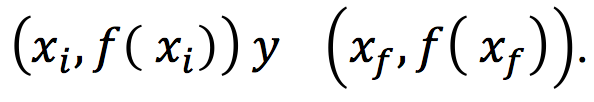 
Pendiente de la recta secante: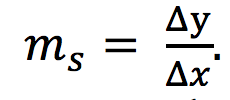 
Recta tangente: es la posición límite de las rectas secantes cuando Δx tiende a cero.
Pendiente de la recta tangente:
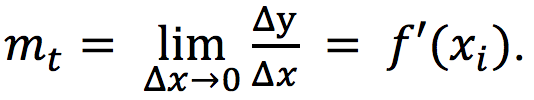(Gráfico 02)
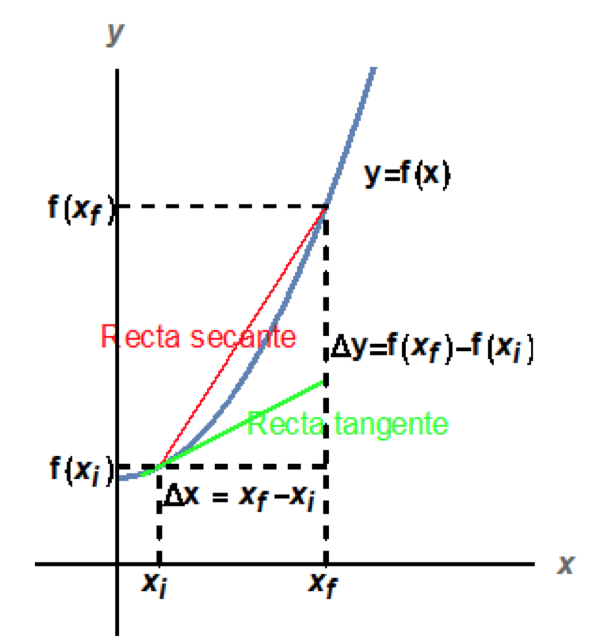Gráfico 02: Secante y tangente
Fuente: Elaboración propia
IV. Resultados y objetivos
A. Planteo de objetivos
Se planteó como objetivo general la evaluación del aprendizaje del concepto de derivada de los alumnos de Análisis Matemático I (AMI).
Y como objetivos específicos la evaluación en tres contextos concretos:
1. El contexto geométrico
2. El contexto físico, velocidad de un móvil
3. El contexto físico, volumen de un gas
B. Tareas para evaluar concepto de derivada
Con el fin de cumplimentar con los objetivos específicos se plantearon tres tareas que reflejan las aplicaciones del concepto de derivada, razón de cambio media e instantánea para los contextos previamente mencionados. Cada una de ellas tiene dos ítems para responder. Todas las actividades están presentadas en formato de respuesta de selección múltiple, siendo una sola de ellas la correcta.
Tarea para el contexto geométrico
Esta tarea está relacionada con los conceptos de recta secante y de recta tangente; es decir, la interpretación geométrica de la derivada. Se pretende evaluar si el alumno distingue la razón de cambio media usando la pendiente de la recta secante y la razón de cambio instantánea a través de la pendiente de la recta tangente.
Tarea 1 (Contexto geométrico)
Sea la función:
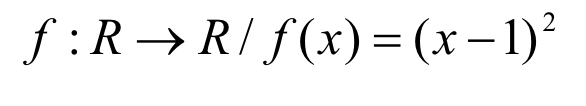
A: Sean los puntos P (2,1) y Q (3,4) de la función f. Siendo “ms” el valor de la pendiente de la recta secante que une P con Q, el mismo representa:
a) La razón de cambio instantánea en el intervalo [2,3]
b) La razón de cambio instantánea en el intervalo [1,4]
c) La razón de cambio media en el intervalo [2,3]
d) La razón de cambio media en el intervalo [1,4]
B: ¿En qué punto la función f tiene como tangente a la recta y = -6x+6?
a) En P (-2,9)
b) En P (-2, 18)
c) En P (1,0) y Q (-5,36)
d) En ningún punto
Las respuestas correctas son: Ac) Bd)
Tarea para el contexto físico, velocidad de un móvil
La tarea de este contexto es un problema de caída libre de una piedra con velocidad inicial distinta de cero. Esta selección se debe a que cuestiones sobre velocidad de objetos o móviles está presente en varios libros de texto y tiene vinculación con la asignatura Física. Aquí es preciso ser riguroso con las unidades de las variables independiente y dependiente. Se intenta evaluar la obtención de la ecuación de la velocidad a través de la derivación de la ecuación de la posición de acuerdo con el sistema de referencia presentado. También el cálculo de la velocidad con la cual la piedra llega al piso y el tiempo empleado para hacerlo.
Tarea 2 (Contexto físico, velocidad de un móvil)
Se arroja hacia abajo una piedra desde 1600 metros de altura con una velocidad inicial de . Considerando 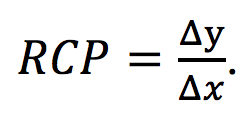y un sistema de referencia con origen a los 1600 metros y con sentido positivo hacia abajo, la ecuación de la posición es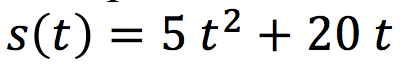 
A: La ecuación de la velocidad de acuerdo con el sistema de referencia es:
a) v(t) = 10 t + 20
b) v(t) = 10 t – 20
c) v(t) = -10 t + 20
d) v(t) = -10 t – 20
B: La piedra llega al piso aproximadamente:
a) A los 16 segundos y con una velocidad de 180 m/s
b) A los 16 segundos y con una velocidad de -180 m/s
c) A los 17 segundos y con una velocidad de 180 m/s
d) A los 17 segundos y con una velocidad de -180 m/s
Las respuestas correctas son: Aa) Ba)
Tarea para el contexto físico, volumen de un gas
Esta tarea se refiere a la relación entre el volumen de un gas con respecto a la presión. La razón de inclusión de ésta es que la relación entre las variables es inversamente proporcional. Aquí también es preciso ser riguroso con las unidades de las variables independiente y dependiente. Se procura evaluar si el alumno distingue y calcula las razones de cambio media e instantánea, a partir de ciertos datos numéricos.
Tarea 3 (Contexto físico, volumen de un gas)
La siguiente tabla corresponde a los valores de la variación del volumen de un gas (medido en litros) respecto a la presión (medida en Pascales) en el intervalo [1,10]:
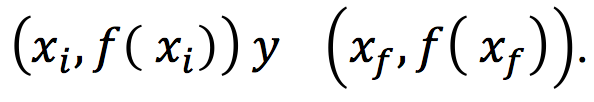
A: ¿Cuál de las siguientes fórmulas representa la tasa de variación instantánea en un punto?
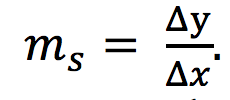
B: ¿Cuál es la variación media del gas si la presión aumenta de 2 a 6 Pascales?
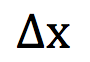
Las respuestas correctas son: Ab) Bc)
C. Resultados
La evaluación se llevó a cabo en los cuatro cursos de AMI que las autoras tienen a cargo. Se realizó vía Internet, utilizando la aplicación gratuita de la plataforma Google Drive, denominada Formularios. Los alumnos trabajaron en grupos de dos estudiantes y obtuvimos 128 respuestas (256 estudiantes).
Los resultados obtenidos para la tarea del contexto geométrico se visualizan en el Gráfico 03.
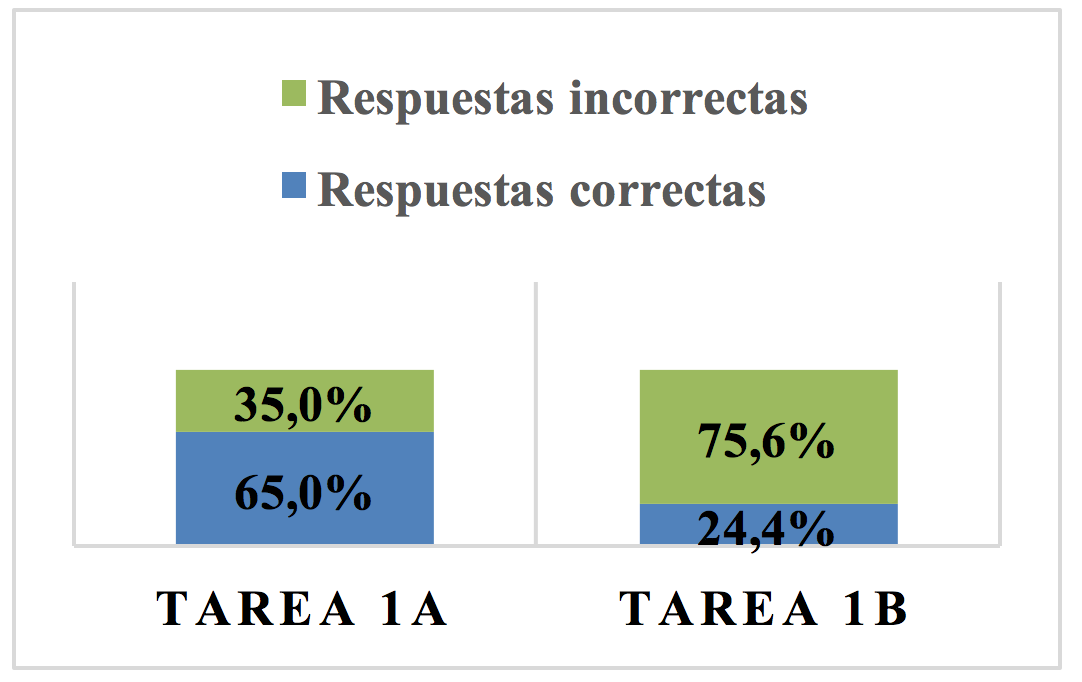Gráfico 03: Resultado tarea 1
Fuente: Elaboración propia
Los de la tarea del contexto físico, velocidad de un móvil Gráfico 04.
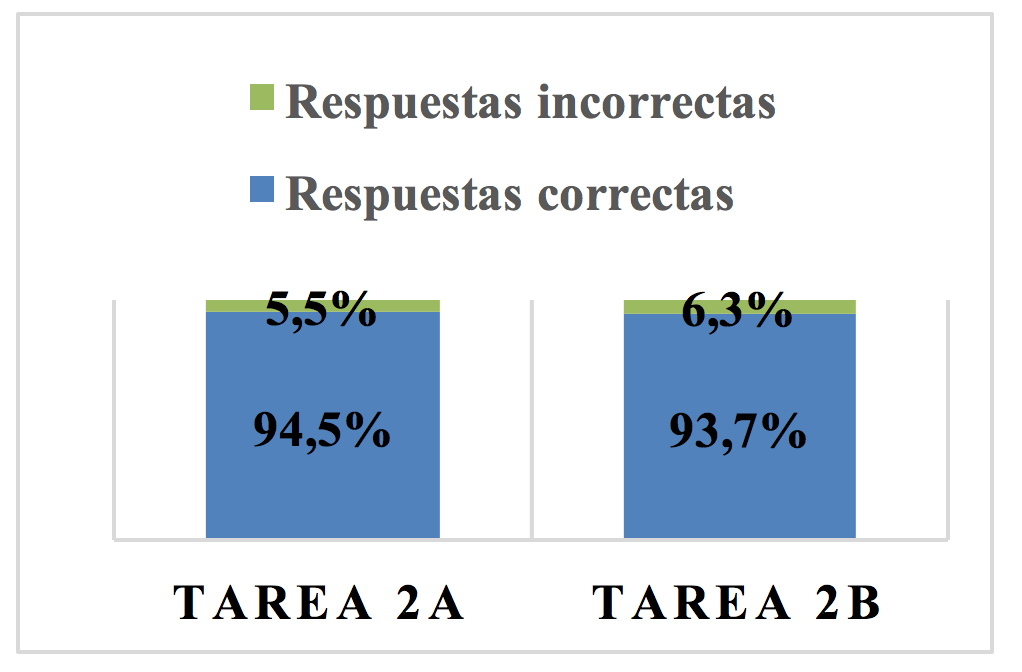Gráfico 04: Resultado tarea 2
Fuente: Elaboración propia
Los de la tarea del contexto físico, volumen de un gas, en el Gráfico 05.
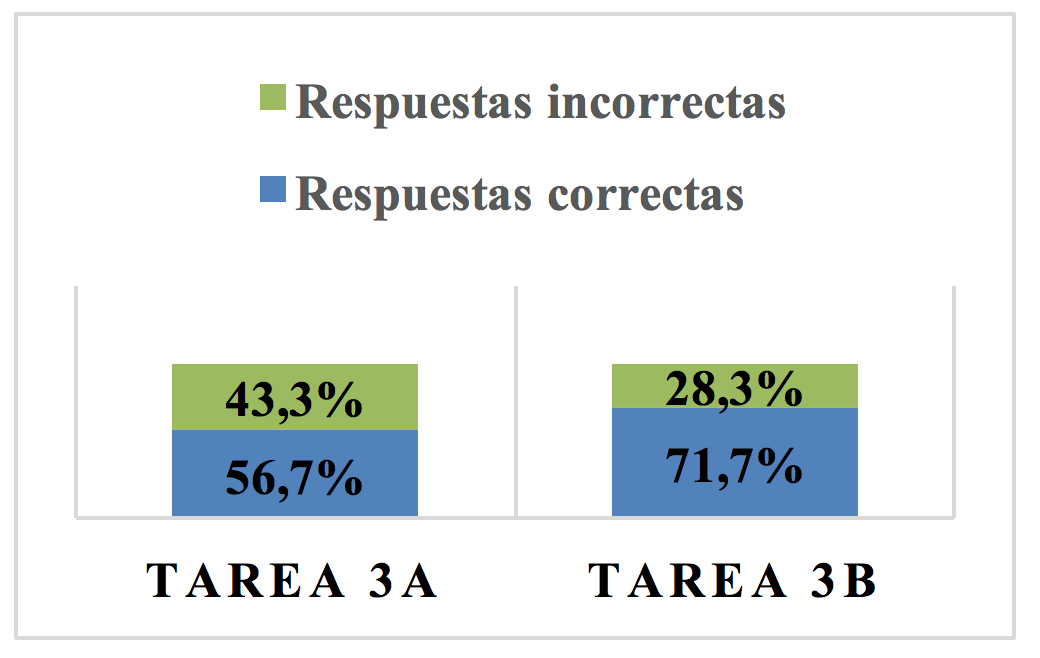Gráfico 05: Resultado tarea 3
Fuente: Elaboración propia
V. Discusión
Los niveles de conocimiento sobre la aplicación del concepto de derivada en el contexto geométrico son regulares, sobre todo en la opción B. En el contexto físico relacionado con la velocidad de un móvil los resultados fueron satisfactorios. Y en la tarea del contexto físico, vinculada al volumen de un gas, los niveles de desempeño resultaron moderados para los dos ítems.
En el último proyecto de investigación, con vigencia 2016-2017, se observaron bajos niveles de aprendizaje del concepto de derivada en los alumnos de la cátedra AMI, coincidiendo con los resultados de varios estudios sobre la enseñanza y aprendizaje del Cálculo [8],[9],[10],[11],[12]. En dicha investigación se trabajó con distintos contextos y uno de los resultados obtenidos fue que los alumnos no podían explicar en cada uno el significado de la RCP o RCI, lo que motivó a evaluar el concepto en tres contextos, el geométrico, el físico con velocidad de un móvil y el de volumen del gas.
Estos resultados brindan un punto de partida concreto para iniciar la siguiente tarea del proyecto, es decir el diseño del recurso didáctico y utilización en el proceso de enseñanza aprendizaje. Luego, se repetirá esta evaluación y se compararán los resultados. Por lo tanto, esta primera evaluación es esencial para establecer si el uso de la aplicación GeoGebra como recurso didáctico para resolver tareas relacionadas con el concepto de derivada resulta eficaz.
VI. Conclusiones
Se han logrado diseñar tareas para evaluar el aprendizaje del concepto de derivada de los alumnos de AMI, específicamente en tres contextos concretos:
1. El contexto geométrico
2. El contexto físico, velocidad de un móvil
3. El contexto físico, volumen de un gas
En dichas tareas el énfasis está en los conceptos de razones de cambio media e instantáneas.
En cuanto a los resultados obtenidos podemos afirmar que los niveles de aprendizaje del concepto de los alumnos de la cátedra presentan disparidades, ya que en los contextos físicos los valores obtenidos fueron mejores que en el contexto geométrico.
Se considera que el diseño de estas tareas como un aspecto fundamental para el proyecto, dado que el conocer los niveles iniciales de aprendizaje del concepto de derivada de los alumnos de AMI del DIIT de UNLaM al resolver tareas en diferentes contextos, facilita la elaboración de actividades que podrían ser aptas a incluir en el recurso didáctico utilizando la aplicación GeoGebra. Se espera que, luego de la utilización del recurso didáctico, el aprendizaje del concepto de derivada de los alumnos de AMI, sea sensiblemente mayor.
VII. Referencias y bibliografía:
[1] Stewart, J. (1999). Cálculo conceptos y contextos. México: International Thomson Editores.
[2] Ruiz, A. y Barrantes, H. (1997). Elementos de Cálculo diferencial. Volumen 1, Límites y derivadas. Costa Rica: Editorial de la Universidad de Costa Rica.
[3] Thomas, G., Finney, R. y Weir, M. (1998). Cálculo de una variable. 9na ed. México: Addison Wesley Longman, Inc.
[4] Klaf, A. (1944). Calculus Refresher. New York: Dover Publications, Inc.
[5] CONFEDI, (2014). Competencias en Ingeniería. 1ra ed. Mar del Plata: Universidad FASTA.
[6] Blanco, L. (1993). “Una clasificación de problemas matemáticos”, Épsilon, nro. 25m pp. 49-60.
[7] Abálsamo, R., Beiró, A., Mastucci, S., Quirós, N y De Rossi, F. (2013). Matemática 4: ¿para qué sirve?: versión para el docente. Boulogne. Puerto de Palos. 256 p.
[8] Azcárate, C. (1990). “La velocidad: introducción al concepto de derivada”, tesis doctoral, Universidad Autónoma, Barcelona.
[9] Clark. J., Cordero, F., Cottrill, J., et al, (1997). “Constructing a schema: the case of the chain rule”, II Journal of Mathematical Behavior vol. 14, no. 4, pp. 345–364.
[10] Dolores, C. (1998). “Algunas ideas que acerca de la derivada se forman los estudiantes del bachillerato en sus cursos de Cálculo Diferencial”, en F. Hitt (Ed.), Investigaciones en Matemática Educativa II, pp. 257-272. México: Grupo Editorial Iberoamérica.
[11] B. Baker, L. Cooley & M. Trigueros. (2000). “A calculus graphing schema”, The Journal for Research in Mathematics Education vol. 31, no. 5, pp. 557–578.,
[12] G. Sánchez–Matamoros, (2004). “Análisis de la comprensión en los alumnos de bachillerato y primer año de la universidad sobre la noción matemática de derivada (desarrollo del concepto)”, tesis doctoral, Universidad de Sevilla, España.
Recibido: 2019-02-26
Aprobado: 2019-06-11
Datos de edición: Vol.4 - Nro.1 - Art.4
Fecha de edición: 2019-06-28
URL: http://www.reddi.unlam.edu.ar
| |