| |
Artículo Original
Diseño automático de un clasificador para filtrado de ruido en imágenes binarias utilizando análisis discriminante lineal
Automatic design of a classifier for noise filtration in binary images using linear discriminant analysis
Susana GUEVARA, Emilio ROBALINO, Agustina BOUCHET, Marcel BRUN, Virginia BALLARIN
Laboratorio de Procesamiento de Imágenes,
Instituto de Investigaciones Científicas y Tecnológicas en Electrónica (ICYTE - CONICET),
Facultad de Ingeniería. Universidad Nacional de Mar del Plata.
vballari@fi.mdp.edu.ar
Resumen:
El siguiente trabajo presenta el diseño automático de un clasificador para filtrado de ruido en imágenes binarias utilizando la técnica del análisis discriminante lineal. Se diseñó el clasificador en dos etapas: entrenamiento y testeo. En la etapa de entrenamiento, utilizando un conjunto de n-pares de imágenes con ruido aditivo al 10%, se obtuvo una matriz de observaciones con sus respectivas etiquetas para una ventana de tamaño 3x3 y 5x5. Aplicando la técnica del análisis discriminante lineal se consiguió un conjunto de coeficientes generando un nuevo filtro que es el que se propone en este trabajo. En la etapa de testeo se comparó el clasificador propuesto con un filtro heurístico, en este caso se eligió el filtro mediana. Ambos fueron aplicados a tres imágenes de prueba con ruido aleatorio al 10%. Se calculó el error cuadrático medio para ambas técnicas. Se concluyó que, para las condiciones experimentales diseñadas, el clasificador propuesto tiene un mejor rendimiento con respecto al filtro mediana.
Palabras Clave: Procesamiento de imágenes, diseño automático, análisis discriminante lineal, filtrado de ruido, imágenes binarias.
Abstract:
In this work, we present an automatic design of a classifier for noise filtering in binary images using linear discriminant analysis. The classifier was designed in two stages: training and testing. In the training stage, we use a set of n-pairs of images with 10% additive noise to obtain a matrix of observations with their respective labels for 3x3 and 5x5 windows. We propose to apply linear discriminant analysis to obtain a set of coefficients in order to define the new filter. In the testing stage, the proposed classifier was compared with a heuristic filter, in this case, the median filter was chosen. Both were applied to different images with random noise. The mean square error was calculated. The proposed classifier has a better performance with respect to the median filter for the experimental conditions designed.
Key Words: Image processing, automatic design, linear discriminant analysis, noise filtering, binary images.
I. Contexto
Este trabajo fue realizado en el Laboratorio de Procesamiento de Imágenes del Instituto de Investigaciones Científicas y Tecnológicas en Electrónica (ICYTE), Universidad Nacional de Mar del Plata y financiado por el Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET).
II. Introducción
El diseño automático consiste en una optimización estadística utilizando ejemplos de entrenamiento. Cada ejemplo de entrenamiento se compone de una imagen observada, es decir una imagen con el problema a resolver, y una imagen ideal que es la imagen deseada después del procesamiento. El diseño y la representación de dichos filtros se realiza utilizando grandes tablas de decisión y clasificadores lineales clásicos [1].
El análisis discriminante lineal (LDA, siglas en inglés) es una técnica para resolver problemas de reducción de dimensionalidad como un paso de pre-procesamiento para aprendizaje automático y clasificación de patrones. En este trabajo se realizó la construcción de un clasificador a partir de un conjunto de observaciones etiquetadas que separará las clases predefinidas lo mejor posible y así, poder predecir las clases de una nueva observación no etiquetada. [2]
a. Desarrollo del LDA
El análisis discriminante lineal es una técnica utilizada en estadística, reconocimiento de patrones y aprendizaje automático para encontrar una combinación lineal de características que separa dos o más clases de objetos o eventos. La combinación resultante se puede usar como un clasificador lineal o para la reducción de dimensionalidad antes de una clasificación [3].
El objetivo del LDA es proyectar la matriz de datos originales sobre un espacio dimensional reducido. Para lo lograr este objetivo, cuatro pasos necesitan ser desarrollados y se describen a continuación.
El primer paso es calcular la separabilidad entre las diferentes clases (o las distancias entre las medias de las diferentes clases), que es llamada varianza entre clases SB y se define como [2]:
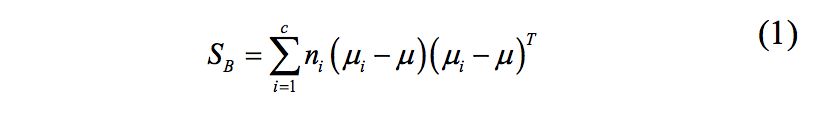
donde c es el número total de clases, ni es el número de observaciones por clase, µi es la media por clase y µ es la media total.
El segundo paso es calcular la distancia entre la media y las muestras de cada clase, que es llamada varianza dentro de clase SW y se define como [2]:
donde Xij representa el i-ésimo vector de observación correspondiente a la j-ésima clase, conformado por valores de 0 y 1.
El tercer paso es construir el espacio dimensional reducido que maximiza la varianza entre clases y minimiza la varianza dentro de clase. Para determinar el espacio dimensional reducido W se calcula la matriz de transformación utilizando el criterio de Fisher definido a continuación [4],[5]:
Cada componente de la matriz corresponde a los coeficientes de discriminación.
El cuarto paso es el cálculo de la constante de discriminación W0 definida como [6]:
donde n1 y n2 son los números de observaciones de cada clase y µ1 y µ2 son las medias de cada clase.
Finalmente se calcula la función discriminante lineal g(x) y se define como [7]:
donde xi representa el i-ésimo vector de observación.
III. Métodos
El experimento desarrollado consiste en el filtrado de ruido de imágenes binarias utilizando la técnica del análisis discriminante lineal desarrollado en dos etapas: una etapa de entrenamiento y una etapa de testeo. Las mismas se detallan a continuación.
a. Etapa de entrenamiento
Del conjunto total de imágenes binarias, observadas e ideales, se seleccionaron aleatoriamente n-pares de imágenes para entrenamiento y de la misma forma para testeo.
Las imágenes observadas presentan ruido aditivo al 10%, mientras que las imágenes ideales son las observadas carentes de ruido como se muestra en la figura 1.
 Fig. 1. Ejemplo de imagen observada e ideal. (a) Imagen observada. (b) Imagen ideal.
Fig. 1. Ejemplo de imagen observada e ideal. (a) Imagen observada. (b) Imagen ideal.
1. Regla Plug in.
En base a los n pares de imágenes se realiza la configuración de ventana conjunta de tamaño d igual a 3x3 y 5x5, obteniendo 2d configuraciones de ventana o vectores de observación. A partir de estos vectores se obtienen dos listas de frecuencias freq(X,Y=0) y freq(X,Y=1) por cada par de imágenes de entrenamiento, la primera cuando el píxel central de la ventana es 0 en la imagen ideal y la segunda cuando el píxel central es 1, respectivamente. Se suma todas las frecuencias por cada clase obteniendo las frecuencias totales, freqT(X, Y=0) y freqT(X,Y=1). Con estas últimas se determina los valores de la función característica ΨN(X) de cada vector de observación analizando cual tiene mayor frecuencia, ΨN(X)=1 si freqT(X,Y=1) > freqT(X,Y=0) y ΨN(X)=0 en el caso contrario. Los valores de la función característica ΨN(X) corresponden a la clase o etiqueta de cada vector de observación.
Por lo tanto, aplicando esta regla se obtuvo una matriz de 512 y 33554432 vectores de observación con su respectiva etiqueta para cada una de las ventanas.
Estos vectores de observación se agruparon de acuerdo con su clase (0 y 1) para el cálculo de la media por clase, la varianza entre clases y la varianza dentro de clase (ecuaciones 1 y 2), el espacio dimensional W que corresponde a un conjunto de coeficientes (ecuación 3) y la constante W0 (ecuación 4).
En la tabla I a manera de ejemplo se presenta un conjunto de coeficientes determinados por la técnica LDA.
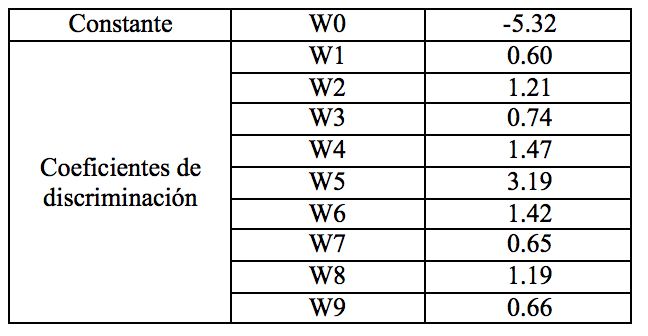 TABLA I.
CONSTANTE Y COEFICIENTES OBTENIDOS EN LA ETAPA DE ENTRENAMIENTO CON 20 PARES DE IMÁGENES PARA UNA VENTANA 3X3 CON LA TÉCNICA DEL LDA.
TABLA I.
CONSTANTE Y COEFICIENTES OBTENIDOS EN LA ETAPA DE ENTRENAMIENTO CON 20 PARES DE IMÁGENES PARA UNA VENTANA 3X3 CON LA TÉCNICA DEL LDA.
b. Etapa de testeo
Con los coeficientes obtenidos en la etapa de entrenamiento se construyó un filtro de igual tamaño que la ventana utilizada. Cada imagen de prueba con ruido aditivo al 10% convoluciona con este filtro, sumando a este resultado la constante W0. Con esto se calcula la función discriminante g(x) dada en la ecuación (5), que toma los siguientes valores: Si g(x) >0 entonces el pixel central pertenece a la clase 1, caso contrario pertenece a la clase 0.
Para evaluar el desempeño del clasificador diseñado se calculó el error cuadrático medio definido a través de la siguiente ecuación:
donde n corresponde al número total de píxeles de X1(imagen original) que tiene el mismo tamaño que X2(imagen testeada).
Este error permite estimar la capacidad de clasificación del operador diseñado cuando se aplica a nuevas imágenes del problema en cuestión [1].
IV. Resultados
En esta sección, presentamos los resultados de la aplicación del clasificador diseñado. Como se muestra en la tabla II, el error del clasificador para una ventana de tamaño 3x3 se estabiliza a partir de 2 pares de imágenes. Por tal motivo se realiza un análisis exhaustivo para una ventana de tamaño mayor 5x5.
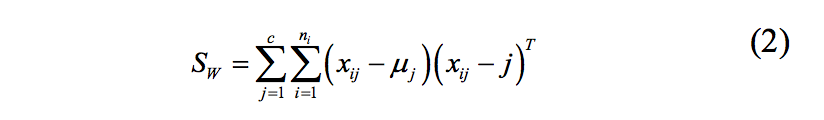 TABLA II.
Error cuadrático medio para 1, 2 y 20 pares de imágenes de entrenamiento con una ventana de tamaño 3x3.
TABLA II.
Error cuadrático medio para 1, 2 y 20 pares de imágenes de entrenamiento con una ventana de tamaño 3x3.
En la figura 2 se muestran las tres imágenes sobre las cuales se va a aplicar el filtrado. En las figuras 3, 4 y 5 se muestran los resultados del filtrado de ruido con diferentes pares de imágenes de entrenamiento, 20, 30, 40, 50, 60 y 100, respectivamente para una ventana de tamaño 5x5. Para una mejor visualización de los resultados se presenta una porción de cada imagen de prueba de tamaño 50x50 píxeles.
En las tablas III a VIII se presenta el error cuadrático medio del clasificador y el error cuadrático medio del filtro mediana para una ventana de tamaño 5x5 con diferentes pares de imágenes de entrenamiento, para las tres imágenes de prueba. Estos errores son representados mediante diagramas de cajas en las figuras 6 a 11.
En la figura 12, se muestran los diferentes errores del clasificador en función del número de imágenes de entrenamiento para una ventana de tamaño 5x5.
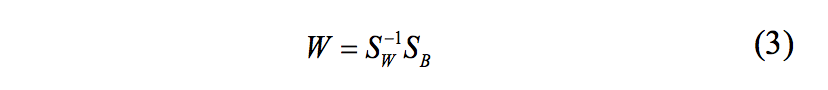 Fig. 2. Imágenes de prueba para filtrado. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 2. Imágenes de prueba para filtrado. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
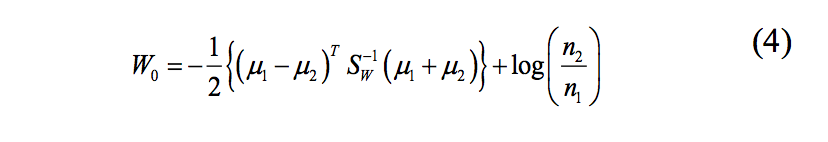 Fig. 3. Filtrado de la imagen de prueba 1. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) Imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
Fig. 3. Filtrado de la imagen de prueba 1. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) Imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
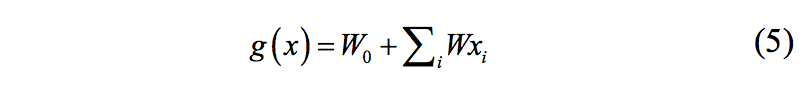 Fig. 4. Filtrado de la imagen de prueba 2. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
Fig. 4. Filtrado de la imagen de prueba 2. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
 Fig. 5. Filtrado de la imagen de prueba 3. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) Imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
Fig. 5. Filtrado de la imagen de prueba 3. (a) Imagen ideal. (b) Imagen ruidosa. (c)-(h) Imágenes filtradas con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento, respectivamente para una ventana de tamaño 5x5.
 TABLA III.
ERROR CUADRÁTICO MEDIO PARA 20 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA III.
ERROR CUADRÁTICO MEDIO PARA 20 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
 TABLA IV.
ERROR CUADRÁTICO MEDIO PARA 30 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA IV.
ERROR CUADRÁTICO MEDIO PARA 30 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
 TABLA V.
ERROR CUADRÁTICO MEDIO PARA 40 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA V.
ERROR CUADRÁTICO MEDIO PARA 40 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
 TABLA VI.
ERROR CUADRÁTICO MEDIO PARA 50 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA VI.
ERROR CUADRÁTICO MEDIO PARA 50 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
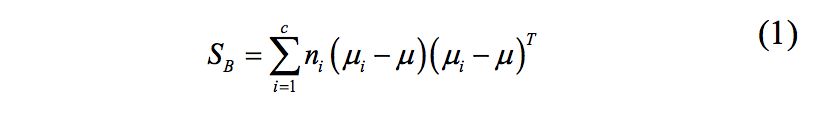 TABLA VII.
ERROR CUADRÁTICO MEDIO PARA 60 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA VII.
ERROR CUADRÁTICO MEDIO PARA 60 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
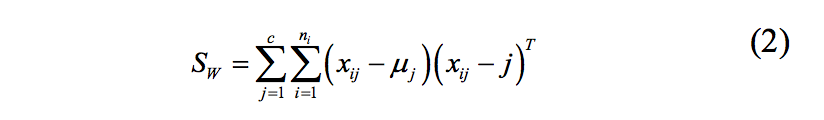 TABLA VIII.
ERROR CUADRÁTICO MEDIO PARA 100 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
TABLA VIII.
ERROR CUADRÁTICO MEDIO PARA 100 PARES DE IMÁGENES DE ENTRENAMIENTO CON UNA VENTANA DE TAMAÑO 5X5.
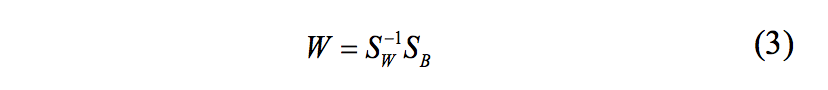 Fig. 6. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 20 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 6. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 20 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
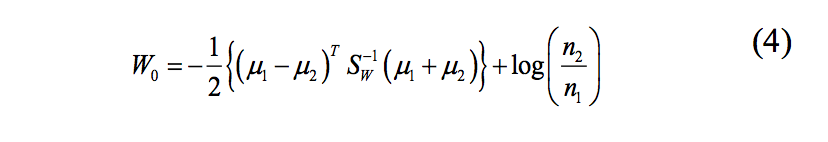 Fig. 7. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 30 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 7. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 30 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
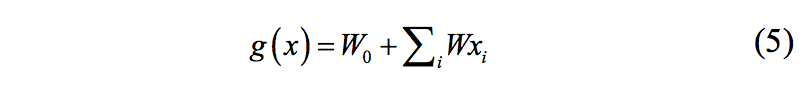 Fig. 8. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 40 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 8. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 40 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
 Fig. 9. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 50 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 9. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 50 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
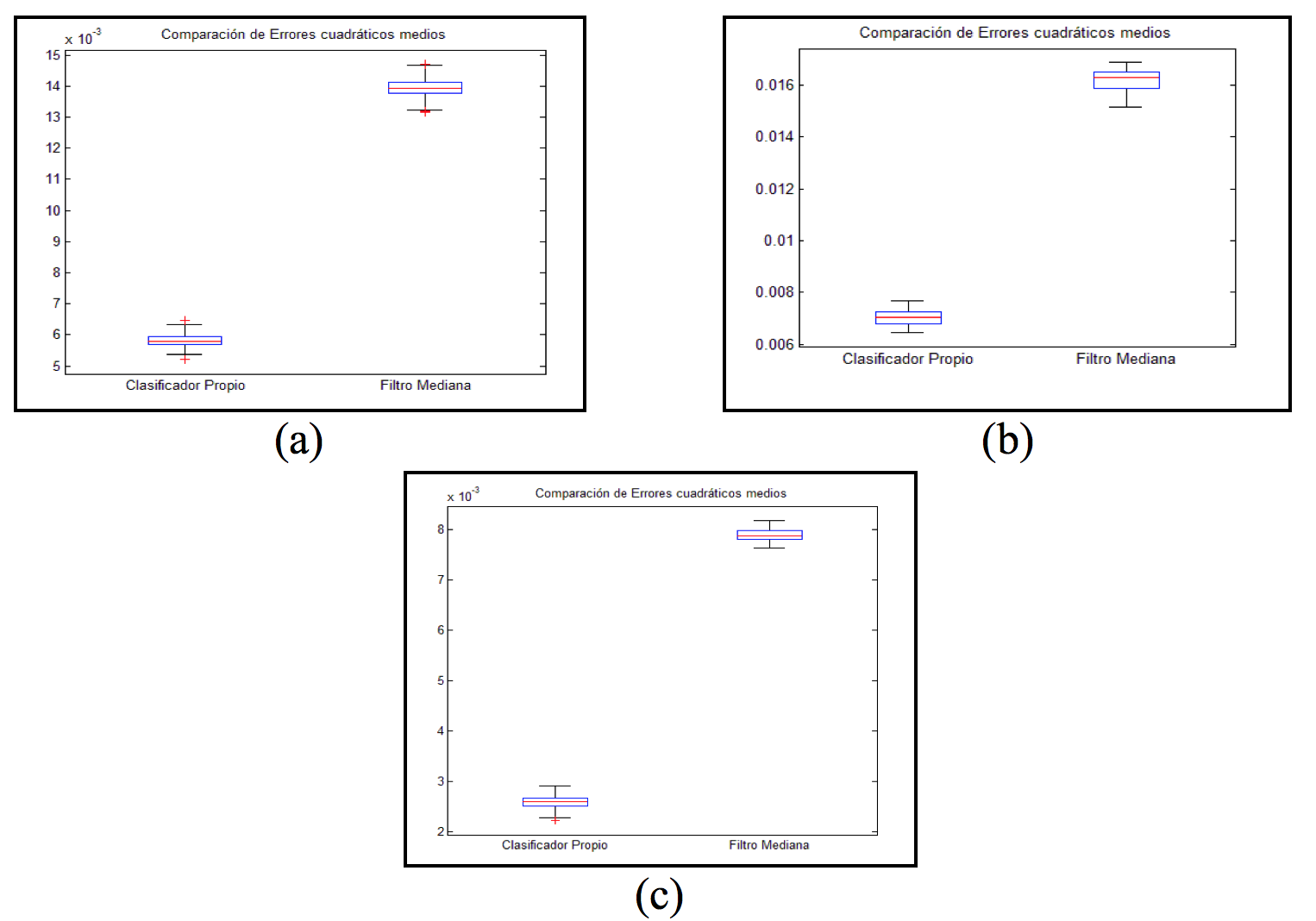 Fig. 10. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 60 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 10. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 60 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
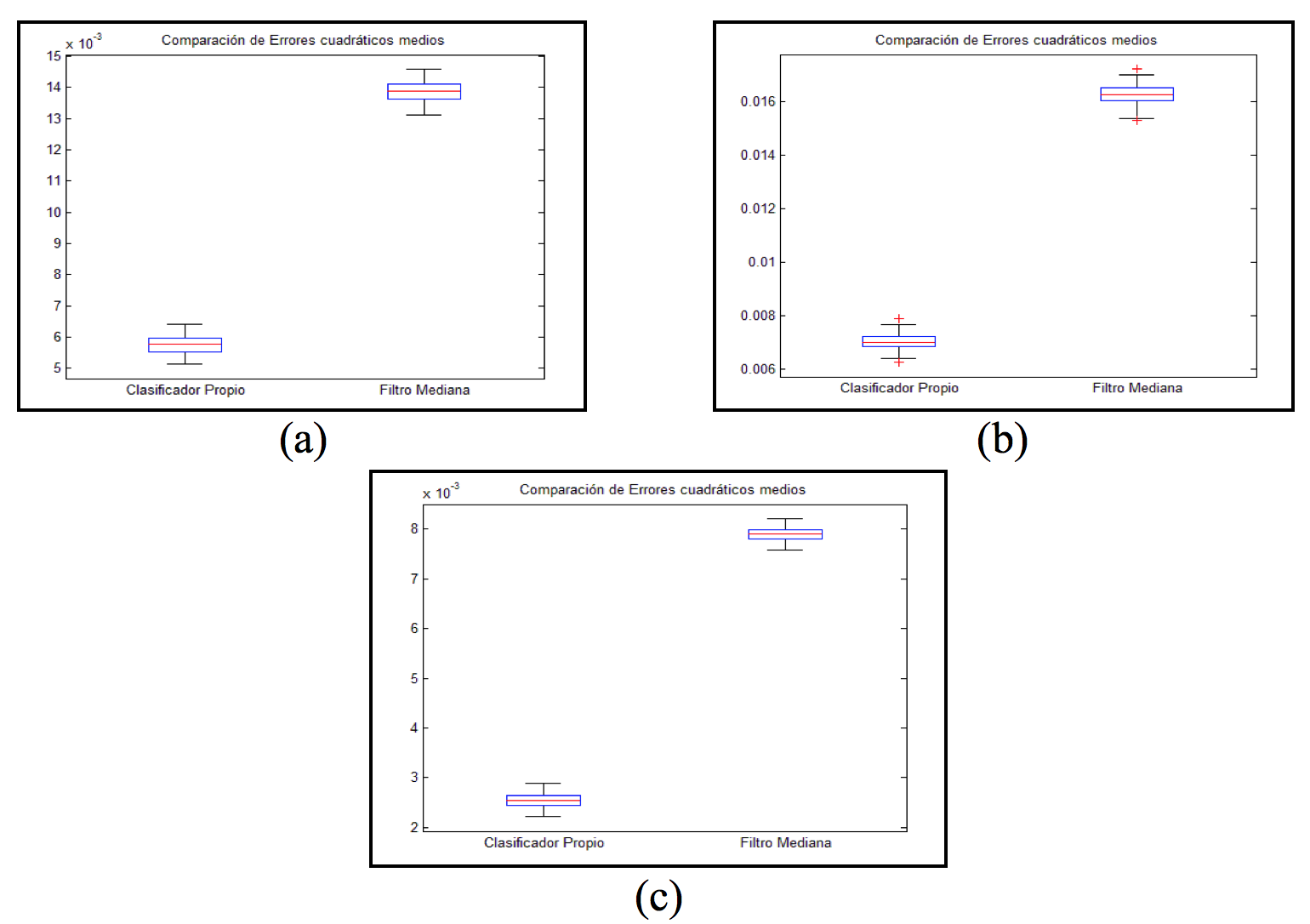 Fig. 11. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 100 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
Fig. 11. Diagrama de caja del error cuadrático medio para el clasificador LDA (caja izquierda) y filtro mediana (caja derecha) con 100 pares de imágenes de entrenamiento y una ventana de tamaño 5x5. (a) Imagen 1. (b) Imagen 2. (c) Imagen 3.
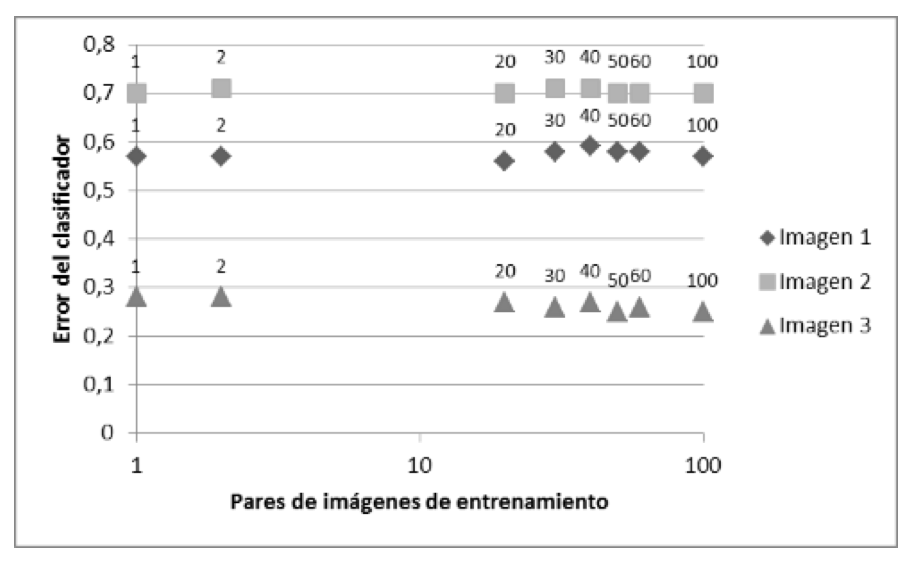 Fig. 12. Error del clasificador para una ventana de tamaño 5x5 en función del número de imágenes de entrenamiento.
Fig. 12. Error del clasificador para una ventana de tamaño 5x5 en función del número de imágenes de entrenamiento.
V. Discusión
El menor error cuadrático medio para 1, 2 y 20 pares de imágenes de entrenamiento con una ventana de tamaño 3x3 usando el clasificador LDA es 0.29%, 0.25% y 0.26%, respectivamente mientras que para el filtro mediana es 0.73%, 0.73% y 0.72%.
El menor error cuadrático medio para 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento con una ventana de tamaño 5x5 usando el clasificador LDA es 0.27% ± 2.07e-06, 0.26% ± 1.61e-06, 0.27% ± 1.93e-06, 0.25% ± 1.76e-06, 0.26% ± 2.23e-06 y 0.25% ± 2.07e-06, respectivamente, mientras que para el filtro mediana es 0.79% ± 1.00e-06, 0.79% ± 6.81e-07, 0.79% ± 1.40e-06, 0.79% ± 1.44e-06, 0.79% ± 1.56e-06 y 0.79% ± 1.49e-06.
La figura 12 muestra que el error cuadrático medio del clasificador para una ventana de tamaño 5x5 no posee diferencias significativas cuando incrementa el número de pares de imágenes de entrenamiento. Esto indica que, para 20 pares de imágenes de entrenamiento en adelante, el error del clasificador permanece estable.
En las figuras 6 a 11, los diagramas de cajas muestran una diferencia significativa entre el error cuadrático medio del clasificador LDA y el error cuadrático medio del filtro mediana para una ventana 5x5 con 20, 30, 40, 50, 60 y 100 pares de imágenes de entrenamiento siendo menor para el clasificador LDA en todos los casos.
VI. Conclusiones
En este trabajo se presentó al LDA como instrumento para el diseño de un clasificador para filtrado de ruido en imágenes binarias. La aplicación del clasificador diseñado mostró mejor rendimiento con respecto al filtro mediana para las condiciones experimentales diseñadas.
Se puede concluir que para el entrenamiento del clasificador es suficiente 20 pares de imágenes para una ventana de tamaño 5x5 ya que el error del clasificador a partir de ese número de pares de imágenes se estabiliza.
Como trabajo futuro se propone aplicar este mismo análisis para extracción de bordes en imágenes binarias, así como también, para el filtrado de ruido en imágenes en niveles de gris.
VII. Referencias:
M. Benalcázar, “Aprendizaje computacional y morfología matemática aplicados al procesamiento de imágenes biomédicas”, Tesis Doctoral, Universidad Nacional de Mar del Plata, Argentina, 2014.
[2] A. Tharwat, T. Gaber, A. Ibrahim, and A. E. Hassanien, "Linear discriminant analysis: A detailed tutorial", AI Communications, vol. 30, no 2, pp. 169-190, May 2007.
[3] C. Li, and W, Bingyu. (2014, August 31). Fisher Linear Discriminant Analysis. [en línea], Available: https://pdfs.semanticscholar.org/1ab8/ea71fbef3b55b69e142897fadf43b3269463.pdf.
[4] R. A. Fisher, “The use of multiple measurements in taxonomic problems”. Annals of eugenics, vol. 7, no 2, pp. 179-188, September 1936.
[5] Sugiyama, M., "Local fisher discriminant analysis for supervised dimensionality reduction" in Proceedings of the 23rd international conference on Machine learning, Pittsburgh, Pensylvania, pp. 905-912, June 2006.
[6] D. Zhang, X. Jing, and J. Yang, Biometric image discrimination technologies, USA, IGI Global, 2006.
[7] A. J. Izenman, Modern multivariate statistical techniques. Regression, classification and manifold learning, USA, Springer, 2008.
Recibido: 2019-04-30
Aprobado: 2019-06-18
Datos de edición: Vol.4 - Nro.1 - Art.3
Fecha de edición: 2019-06-28
URL: http://www.reddi.unlam.edu.ar
| |