| |
Artículo Original
Rough set theory y conexiones de galois en contextos formales
Rough set theory and galois connections in formal context
Osvaldo Jorge GALARDO
Universidad Nacional de La Matanza
ogalardo@gmail.com
Resumen:
Se estudia la relación entre las Conexiones de Galois (CG) y la Rough Set Theory (RST) en Contextos Formales (CF). El objetivo de este trabajo es mostrar la fertilidad teórica que se manifiesta al expresar RST en base a CG en Contextos Formales, ya que las Conexiones de Galois participan en estructuras lógico- matemáticas numerosas e interconectadas y forman parte de la base de la Informática teórica y aplicada. Se analizó la bibliografía específica y se destacó: a) la importancia del Teorema que conecta CG y RST, ya que asegura la ampliación de las aplicaciones de RST como se conjetura en el trabajo; b) El papel del Análisis de Conceptos Formales (Formal Concept Analysis- FCA) en lo conjeturado en a). Las CG, en tanto que relaciones binarias generalizadas, constituyen un puente que conecta tres niveles principales en los sistemas de información: A) computacional; B) algorítmico; C) Implementacional, que se encuentra en el nivel físico del sistema. Además, las Conexiones de Galois permiten expresar la Relación de Indiscernibilidad de RST empleando retículos distributivos y complementados, es decir por medio de Álgebras de Boole.
Palabras Clave: Conexiones de Galois, Rough Set Theory, Análisis de Contextos, Análisis de Conceptos Formales, Teoría de Retículos, Relaciones Algebraicas Generalizadas
Abstract: The relationship between Galois Connections (CG) and Rough Set Theory (RST) in formal context is studied. The aim of this paper is to show the theoretical fertility appears to express RST based on CG in Formal Context, since Galois Connections involved in numerous interconnected logical mathematical structures and form part of the basis of theoretical and applied computer science. The specific bibliography was analyzed resulting the importance of Theorem CG that connects RST in extending the applications of RST. In addition the role of Formal Concept Analysis (FCA Analysis- Formal Concept) is highlighted. The CG, regarded as generalized binary relations constitute a bridge connecting three main levels in information systems: A) computing; B) algorithm; C) Implementational, located at the physical level of the system. Moreover, Galois Connections allow express the Indiscernibility Relation of RST using distributive lattices and complemented; ie through Boole algebras.
Key Words: Galois Connection, Rough Set Theory, Formal Context, Formal Concepts Analysis, Lattices Theory, Generalized Algebraic Relations
La RST (Rough Set Theory) constituye un recurso importante en Minería de Datos (Data Mining), para analizar información imprecisa. Por su parte, las Conexiones de Galois (y sus conexiones con los Contextos Formales y el Análisis de Conceptos Formales) ocupan un lugar destacado en los mapeos entre relaciones de orden aplicadas a sistemas, tal como se entienden en Álgebra Universal. El análisis de las condiciones en que RST se puede expresar por medio de CG, permite explorar la expansión de RST a nuevas aplicaciones como el estudio de sistemas complejos, especialmente del ámbito de la Economía.
La teoría de conjuntos aproximados o rugosos (Rough Set Theory, brevemente: RST) se basa tradicionalmente en relaciones de equivalencia. La literatura disponible [1], [2], [3] exhibe otras formas algebraicas que generalizan su fundamentación y aplicaciones empleando relaciones de orden parcial, en particular las Conexiones de Galois (CG). En este trabajo se evalúa la conexión de RST y CG en el marco algebraico común a ambas y la viabilidad de aplicar RST en los tres niveles principales de los sistemas de información (computacional, algorítmico e implementacional), considerando Contextos Formales y el Análisis de Conceptos Formales.
I. RST ORIGINAL
El rápido incremento [4], [5] de la información producida en ámbitos variados de las ciencias sociales y la industria ha puesto de manifiesto la siguiente paradoja: están disponibles cantidades masivas de datos pero, dado que es frecuentemente incierta e incompleta, el conocimiento extraíble de esa información es conceptualmente pobre.
Además de las técnicas estadísticas clásicas, se han desarrollado distintos métodos analíticos de minería de datos que permiten el descubrimiento de conocimiento vía el refinamiento y la abstracción de datos, la asociación de atributos y la clasificación de características comunes a distintos tipos de objetos.
La Rough Set Theory (RST) fue desarrollada en 1982 por el matemático polaco Zdzislaw Pawlak para trabajar con información en bruto –y, por lo tanto, imprecisa y pobre- sin el requisito de información externa y analizando atributos tanto en calidad como en cantidad.
Pawlak desarrolló su actividad principalmente en el Institute of Theoretical and Applied Mathematics de la Polish Academy of Sciences y el trabajo fundacional de 1982 (Rough Sets) se publicó en el International Journal of Computer and Information Science. Originalmente, el autor presentó RST como alternativa a la Fuzzy Sets Theory y Tolerance Theory, aunque posteriormente se vió que distintas teorías que trabajan con valores aproximados se superponen parcialmente e, incluso, pueden combinarse. Además, RST puede entenderse como una extensión de la Teoría Clásica de Conjuntos y -al igual que CG- está soportada por distintas variedades de Lógica Modal [6].
En particular, RST opera sobre Sistemas de Información que contienen objetos en un espacio asociado, atributos, y las funciones que conectan objetos del espacio con atributos [7].
La idea básica es clasificar la información recurriendo a aproximaciones por exceso y por defecto cuya diferencia es la región frontera; de esta forma se determina, para cada subconjunto de información, si puede ser definido o, en caso contrario, si se tiene una definición aproximada (o no).
Los objetos -según las propiedades en estudio- se evalúan por la relación de indiscernibilidad que determina las clases de elementos indiferenciados y es el fundamento de las aproximaciones en RST.
Las aproximaciones por exceso (o superiores) pueden entenderse como el conjunto de elementos que posiblemente pertenecen al conjunto X del universo U, mientras las aproximaciones por defecto (o inferiores) pueden entenderse como el conjunto de elementos que ciertamente pertenecen a X.
En la formulación original de la teoría, las aproximaciones por exceso y defecto se establecen constructivamente y la relación de indiscernibilidad resulta ser una relación de equivalencia, porque parece razonable sostener que: a) un objeto x es indiscernible de sí mismo (reflexividad); b) si x es indiscernible de y, y lo es de x (simetría); c) si el objeto x es indiscernible de z, y éste de w, entonces resulta evidente que x sea indiscernible de w (transitividad).
Sin embargo, dentro del enfoque constructivo, es posible reformular la Relación de Indiscernibilidad sin recurrir a la reflexividad, la simetría y la transitividad (o sea, como relaciones de equivalencia), empleando -en cambio- relaciones generalizadas retículo-teoréticas [7], en particular las Conexiones de Galois.
RST también admite una fundamentación axiomática [8] en la cual la noción primitiva es el sistema 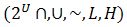 donde donde 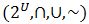 es un álgebra de conjuntos y es un álgebra de conjuntos y 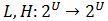 son operadores unitarios sobre el conjunto potencia son operadores unitarios sobre el conjunto potencia 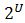 . .
Los operadores de aproximación inferior y superior de la fundamentación constructiva, son aquí los operadores primitivos L y H respectivamente. En esta formulación que la dualidad de los operadores se cumple 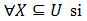 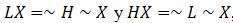 , por lo que podría emplearse sólo uno de los operadores, aunque se emplean ambos por comodidad a la hora de realizar demostraciones más sencillas. , por lo que podría emplearse sólo uno de los operadores, aunque se emplean ambos por comodidad a la hora de realizar demostraciones más sencillas.
Considerando el significado de las aproximaciones por defecto y exceso, se ve que los operadores de aproximación –en la versión axiomática- cumplen un papel similar a los operadores modales de necesidad y posibilidad, por lo que explica que RST puede interpretarse como una extensión de la Teoría de Conjuntos del mismo modo que la Lógica Modal puede entenderse como una extensión de la Lógica Clásica.
II. CONEXIONES DE GALOIS (CG)
Las Conexiones de Galois datan de 1941 y deben su nombre al matemático sueco Oystein Ore, que las presentó en el Meeting de verano de la American Mathematical Society en la Universidad de Chicago [9]. Como lo expresa el autor, se trata de un tipo general de correspondencia entre estructuras y les asignó ese nombre tomándolo de la teoría de ecuaciones de Galois donde la correspondencia entre subgrupos y subcuerpos son un caso particular de CG.
Las Conexiones de Galois pueden expresarse de distintas formas, por ejemplo relaciones binarias o mapeos continuos [9] y debido a la forma general en que operan sobre conjuntos parcialmente ordenados (posets), están presentes en la Teoría de Retículos y en la Teoría de Categorías [10].
También se relacionan con distintas Álgebras Modales y se aplican a Relaciones de Información como en RST (nuestro principal interés), debido a que son especialmente aptas para formalizar las relaciones entre datos concretos y las propiedades abstractas que se asignan a dichos datos (y viceversa). Por ejemplo [11]: ‘5’ como dato concreto puede asignarse a distintos cualidades abstractas (‘número impar’; ‘número entero’; ‘{2,5}’, etc.) y por tal motivo la asignación conlleva pérdida de precisión.
La inversa va de las propiedades abstractas a los datos concretos. Si s es un dato concreto, el mapeo f le asigna una propiedad abstracta y el mapeo g retorna la información contenida en la propiedad abstracta a los datos concretos; en consecuencia, el dato (‘5’ en el ejemplo) pertenece a la composición g con f (aunque inexactamente).
Por lo anterior, las Conexiones de Galois son pares de mapeos que permiten moverse, en ambos sentidos, entre dos estructuras diferentes. Dicho más precisamente: Dos conjuntos parcialmente ordenados (posets) P y Q y el par de mapeos (f,g) tales que 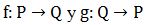 es denominado una Conexión de Galois si: a) para todo es denominado una Conexión de Galois si: a) para todo 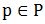 y para todo y para todo 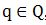 , se cumple: , se cumple: 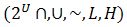 preservan el orden. Esta definición no es la única; en el punto 4) se da la definición alternativa que preserva el orden inverso y es equivalente a la anterior; el empleo de cada una depende de la aplicación deseada. preservan el orden. Esta definición no es la única; en el punto 4) se da la definición alternativa que preserva el orden inverso y es equivalente a la anterior; el empleo de cada una depende de la aplicación deseada.
La función 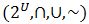 asigna valores a datos concretos (por ejemplo: atributos) y –en este sentido- es un proceso de abstracción. La función asigna valores a datos concretos (por ejemplo: atributos) y –en este sentido- es un proceso de abstracción. La función 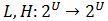 es un proceso de concretización, aunque en todo el circuito se produce pérdida de información [12]. es un proceso de concretización, aunque en todo el circuito se produce pérdida de información [12].
En este punto es necesario puntualizar algunas características de los posets que son relevantes para el tema que se desarrolla.
Brevemente, un conjunto parcialmente ordenado (poset) es el par 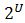 donde donde 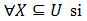 es un conjunto y es un conjunto y 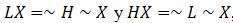 es una relación de orden parcial; o sea que la relación es 1) reflexiva; 2) antisimétrica; 3) transitiva. Formalmente: es una relación de orden parcial; o sea que la relación es 1) reflexiva; 2) antisimétrica; 3) transitiva. Formalmente: 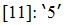 es un poset si es un poset si 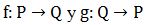 se cumple: se cumple: 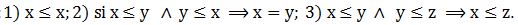
Si el orden es estricto, la relación 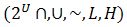 pasa a ser pasa a ser 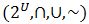 y las relaciones 1) y 2) cambian a: y las relaciones 1) y 2) cambian a: 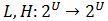 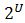 mientras 3) se mantiene. La reflexividad cambia por la arreflexividad y la antisimetría por la asimetría, mientras se mantiene la transitividad mientras 3) se mantiene. La reflexividad cambia por la arreflexividad y la antisimetría por la asimetría, mientras se mantiene la transitividad 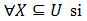 Pero el orden estricto no es aplicable por el motivo siguiente: la función de abstracción Pero el orden estricto no es aplicable por el motivo siguiente: la función de abstracción 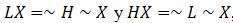 -al preservar el orden parcial- es monótona, pues -al preservar el orden parcial- es monótona, pues 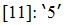 pero aplicar pero aplicar  a la reversa a la reversa  podría dar podría dar  . .
Además, 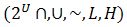 es una inmersión de orden, es decir que es una inmersión de orden, es decir que 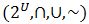 y dicha inmersión asegura que hay una “copia” contenida en la abstracción que preserva el orden. Por otra parte [13] la inmersión de orden de f asegura el isomorfismo de orden entre y dicha inmersión asegura que hay una “copia” contenida en la abstracción que preserva el orden. Por otra parte [13] la inmersión de orden de f asegura el isomorfismo de orden entre 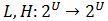 , por lo que , por lo que 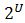 sin similares en relación al orden (o sea, tienen la misma estructura). Y la similaridad de orden asegura que es una relación de equivalencia, ya que se prueba la reflexividad, simetría y transitividad. sin similares en relación al orden (o sea, tienen la misma estructura). Y la similaridad de orden asegura que es una relación de equivalencia, ya que se prueba la reflexividad, simetría y transitividad.
Conviene recordar que los conceptos de similaridad, estructura e inmersión provienen del Álgebra Universal a partir del concepto de Sistema, definido como un triplete que contiene un Universo no vacío y una serie de Relaciones y Funciones definidas sobre dicho Universo [14].
El tipo o signatura del Sistema detalla las funciones y relaciones que operan sobre el Sistema según sus respectivas aridades (monarias, binarias, etc; si la función es 0-aria se trata de un elemento destacado); entonces se dice que dos Sistemas son similares si tienen el mismo tipo o signatura.
Sobre un Sistema se define una estructura especificando las propiedades de las funciones, relaciones y elementos destacados. En particular, un sistema 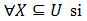 de tipo de tipo 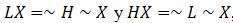 (no contiene funciones y sólo una relación binaria) tiene estructura de retículo si y sólo si (no contiene funciones y sólo una relación binaria) tiene estructura de retículo si y sólo si 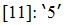 es un orden (es suficiente que sea parcial) y es un orden (es suficiente que sea parcial) y 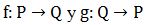 Supremo e Ínfimo de {x,y}. Supremo e Ínfimo de {x,y}.
Dos sistemas pueden estar relacionados de distintas formas: A) que uno sea subsistema de otro, B) Isomorfismo, cuando las estructuras de ambos sistemas coinciden; C) Homomorfismo, cuando las funciones y relaciones mantienen las correspondencias entre los elementos del Universo de un sistema y el Universo del otro; D) Inmersión, cuando un sistema es subsistema isomórfico del otro.
Las estructuras o “universos” y las CG que operan sobre ellas, son frecuentemente abstractos debido a su formulación matemática, pero con una gran variedad de usos teóricos y técnicos; en particular, son conocidas las aplicaciones en computación, como la construcción de programas, procesamiento de la información y análisis de datos [15]. En Sistemas de Información Multivaluados [16], es posible expresar cualidades como relaciones binarias arbitrarias (por ejemplo: similaridad y ortogonalidad).
En particular, también es posible expresar las aproximaciones correspondientes a supremos e ínfimos de RST por medio de dichas relaciones binarias arbitrarias y sus inversas [11].
Más específicamente, puede probarse que los pares de relaciones que expresan las aproximaciones de RST, son Conexiones de Galois en el cardinal del universo U, como se expresa en el punto siguiente.
III. RST y CG
Expresadas como relaciones de equivalencia, las aproximaciones inferiores y superiores en RST se definen:
 donde donde 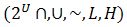 expresa la relación de equivalencia y expresa la relación de equivalencia y 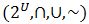 es el conjunto frontera. es el conjunto frontera.
Expresadas por medio de una relación binaria arbitraria las aproximaciones se definen:
- Relación binaria:
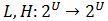
- Aproximación Superior de
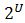
- Aproximación Inferior de
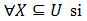
- Como antes, el conjunto frontera es
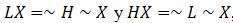
- Las distintas aproximaciones superiores e inferiores inducen la partición de universo U en el Conjunto Potencia de U, denotada
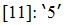
- Por lo anterior,
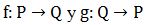
- La inversa de la relación arbitraria se denota R* y se define
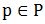
- Para
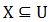 las aproximaciones superior e inferior son, respectivamente, las aproximaciones superior e inferior son, respectivamente, 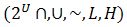 y y 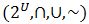
- Si R es simétrica, entonces
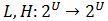
Las nuevas definiciones generalizan las definiciones originales porque R(x) es una relación arbitraria; entonces -dado que las CG se basan en conjuntos parcialmente ordenados (posets)- se requiere el teorema que conecta RST y CG.
- Teorema [17]: para toda relación binaria en el Universo U, los pares
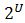 son Conexiones de Galois en son Conexiones de Galois en 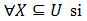 . .
En primer lugar los mapeos 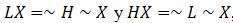 preservan el orden pues si preservan el orden pues si 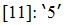 luego resulta que luego resulta que 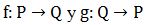 . .
Además, si 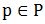 entonces existe y entonces existe y 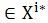 tal que tal que 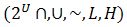 . Debido a que . Debido a que 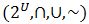 , entonces , entonces 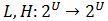 , lo que comprueba que el par , lo que comprueba que el par 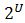 es una Conexión de Galois. En forma similar se prueba que es una Conexión de Galois. En forma similar se prueba que 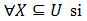 también es una CG. también es una CG.
El Teorema anterior permite extender la aplicación de RST a la Informática ya que las CG tienen numerosas aplicaciones en la construcción de programas, procesamiento de información y análisis de datos [15].
En cierto modo, las CG son la llave que facilita el acceso de RST a nuevas aplicaciones porque son el puente entre RST y el Análisis de Conceptos Formales (Formal Concept Analysis- FCA), como se ve en el apartado siguiente.
IV. RST y FCA
La búsqueda de patrones ocultos en información voluminosa o deficientemente articulada requiere de recursos informáticos, particularmente los referidos a Minería de Datos. Las distintas técnicas empleadas requieren que la percepción, abstracción y representación de problemas complejos consideren la simplificación y control de costos, lo que justifica los métodos de aproximación con tratamiento de la incertidumbre [18].
Las técnicas informáticas actuales asumen que el Mundo está compuesto por gránulos y en cada modelo –como los conjuntos difusos o rugosos- los gránulos pueden ser diferentes.
Considerados como objetos asociables a componentes del Mundo, los gránulos tienen tres propiedades básicas: intrínsecas, externas y de entorno [19], expresables en proposiciones formadas por conceptos que, como tales, tienen una intensión y una extensión.
En esta concepción clásica de los conceptos la intensión corresponde a las propiedades o atributos de dichos objetos y la extensión consiste en el conjunto de objetos o entidades que satisfacen la intensión del mismo.
Objetos, atributos y la relación entre ambos se especifica en la definición de Contexto Formal, que consiste en el triplo (G, M, R) donde G es el conjunto de objetos, M el conjunto de atributos y R la relación de G a M tal que: 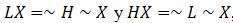 . .
Considerando los conjuntos de partes de G y M se definen los Operadores de Birkhoff [20] de partes de G en partes de M y viceversa: dados los conjuntos arbitrarios G y M , siendo 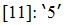 se define se define 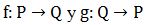 y y 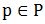
Sea (G, M, R) un contexto formal. El Concepto Formal de dicho contexto formal es el par (A,B) con 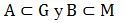 tal que tal que 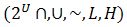
En el contexto formal (G, M, R), el conjunto de todos los conceptos formales de (G, M, R) para los cuales esté definido el orden parcial se denomina concepto reticular de (G, M; R).
En las condiciones anteriores, la 4-upla 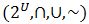 es la Conexión de Galois asociada a (G, M, R). es la Conexión de Galois asociada a (G, M, R).
Con la notación de la 4-tupla anterior la CG está definida en forma antítona, es decir que preserva el orden inverso. La notación monótona dada en el punto 2 aplicada a este caso sería 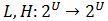 pero aquí no se emplea. pero aquí no se emplea.
Adicionalmente, Pawlak [21] definió lo que aparece como una versión alternativa a los Contextos Formales, que denominó Sistemas de Información (SI).
Más precisamente, un SI relaciona el conjunto de objetos U con el conjunto de valores de los atributos Va, tal que 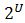 , por lo que en estos Sistemas de Información la conexión entre objetos y atributos es funcional, mientras es relacional en los Contextos Formales. , por lo que en estos Sistemas de Información la conexión entre objetos y atributos es funcional, mientras es relacional en los Contextos Formales.
La informática es un ámbito particularmente fértil para la aplicación de estructuras algebraicas generalizadas en la fundamentación de métodos computacionales empleados para el tratamiento de información con incertidumbre. En particular, las formas generalizadas de RST dan sustento a los desarrollos informáticos que investigan la inteligencia artificial y los sistemas complejos como en los procesos biológicos y económicos. El tratamiento de RST empleando relaciones de orden, tal como se expresan en las Conexiones de Galois, muestra la riqueza conceptual y las posibilidades de nuevos desarrollos y aplicaciones de RST en FCA (Formal Concept Analysis).
El estudio se concentra en los fundamentos teóricos del tema elegido.
Del análisis bibliográfico se concluye que RST admite al menos dos formulaciones equivalentes en su versión constructiva: A) la primera -siguiendo las motivaciones originales- atiende al requerimiento de incluir -en relaciones de equivalencia- información imprecisa; B) la segunda se apoya en la Teoría de Retículos y, al recurrir a posets, emplea relaciones algebraicas generalizadas conectadas con las Álgebras de Boole, debido a su naturaleza retículo-teorética; resulta entonces que el sustento de RST -en este caso- es la formulación monótona de las CG. Por otra parte, la posibilidad de expresar las CG en forma antítona permite la unificación de RST con el Análisis de Conceptos Formales (FCA), lo que justifica la importancia de RST en la Minería de Datos. Por su parte, la formulación algebraica muestra las distintas clases de Álgebras de Conjuntos Rugosos. En la práctica, la forma constructiva es de aplicación más directa debido a que los operadores pueden asociarse intuitivamente con aplicaciones empíricas, pero la formulación algebraica facilita la construcción de algoritmos específicos de cálculo de aproximaciones [8].
V. DISCUSIÓN
RST atendió -en su formulación original- a la necesidad de extraer conocimiento de información voluminosa con dispersión en los datos, lo que ocultaba propiedades de los procesos en estudio. El desarrollo formal de RST mostró conexiones y fundamentos lógicos [22] y algebraicos, que proporcionaron una fértil generalización a la Teoría incluyendo el estudio de objetos complejos con recursos mereológicos [23].
Es importante destacar que la expresión de RST vía CG, extiende sus aplicaciones en dos sentidos: A) con la formulación antítona (o de orden reversa) de CG (que Birkhoff llamó ‘polaridades’) accede al Análisis de Conceptos Formales; B) con la formulación monótona (o isótona, que preserva el orden en forma directa) tiene salida a la Teoría de Categorías pues son consideradas adjunciones y, en consecuencia, pueden establecerse nexos con los functores adjuntos de Kan [15].
Las Conexiones de Galois facilitan la extensión de las aplicaciones de RST debido a que permiten el estudio de Sistemas de Información conectando -en ambos sentidos- objetos y atributos, garantizando la preservación de la relación de orden tanto en la forma isótona como antítona.
VI. CONCLUSIONES
La riqueza expresiva de RST se expresa en dos direcciones complementarias: 1) las conexiones estructurales con teorías conceptualmente potentes como la Teoría de Categorías; 2) la posibilidad de explotar los recursos que proveen metodologías avanzadas de análisis de información como es el caso de las técnicas de soft computing.
En vista de estas cualidades, RST es una opción importante para aplicar al análisis de información económica, en particular para la detección de características o atributos que pueden pasar desapercibidos en la gran cantidad de datos, frecuentemente asistemático.
La viabilidad operativa de las aplicaciones inmediatas de RST, vía CG y FCA, a la Economía (y a los sistemas complejos en general) está basada en la capacidad de procesamiento de datos que provee la Informática por medio de la Teoría de Bases de Datos Relacionales y la Teoría de los Sistemas de Información [24].
La fundamentación teórica de dichas aplicaciones se apoya en métodos aproximados de análisis empleando operadores de aproximación cuantitativos o aún cualitativos [25].
Dichos métodos conectan conjuntos de objetos y conjuntos de atributos por medio de relaciones de indiscernibilidad o relaciones binarias más generales.
En cualquier caso, objetos y atributos son entendidos como los componentes extensionales e intensionales, respectivamente, que expresan -a nivel lingüístico- aspectos relevantes del mundo que se compone de gránulos de información.
La concepción granular y la caracterización de los gránulos remite a Zadeh [26] y evolucionó hasta una teoría informática con extenso desarrollo [19].
Aunque el concepto de gránulos es vago, la aplicación a conjuntos rugosos -y, consecuentemente, en el estudio de sistemas complejos- tiene la ventaja de que: 1) se establecen jerarquías en diferentes niveles de precisión; 2) es factible el tránsito entre niveles y -fundamentalmente- 3) el problema a investigar puede representarse en múltiples niveles de granulación [27].
VII. REFERENCIAS Y BIBLIOGRAFÍA
A. Referencias bibliográficas:
[1] Y.Y. Yao, A Comparative Study of Formal Concept Analysis and Rough Set Teorhy in Data Analysis; en: Tsumato et al. Rough Sets and Current Trends in Computing, 4th International Conference, Upsala; Sweden, Proceedings, Springer-Verlag, Berlín. 2004.
[2] M. Banerjee, M. Chakraborty, Algebra from Rough Sets, en Pal, S. et al.: Rough neural Computing- Techniques for computing with Words, pp. 157-184, Springer-Verlag, Berlín. 2004.
[3] M. Gehrke, E. Walker, On the Structure of Rough Sets, Bulletin of Polish Academy of Sciences, 40: 235-245. 1992.
[4] D. Foray, P. David, “La Sociedad del Conocimiento”, Revista Internacional de Ciencias Sociales, Nº 171. 2002
[5] F. Entonado [coordinador], Sociedad de la Información y Educación, Junta de Extremadura, Consejo de Educación, Ciencia y Tecnología, Mérida. 2001.
[6] J. Järvinen, M. Kondo, J. Kortelainen, “Logics from Galois Connections”, International Journal of Approximate Reasoning, Vol. 49, pp. 595-606. 2008.
[7] Joudi Järvinen (2002): On the Structure of Rough Approximations, Turku Centre for Computer Science, TUCS Technical Report Nº 447, Finlandia. 2002.
[8] Y.Y. Yao, “Constructive and Algebraic Methods of the Theory of Rough Sets”, Information Sciences, Vol.109, Nº 1-4, pp. 21-47. 1998.
[9] Oystein Ore, “Galois Connexions”, Transactions of The American Mathematical Society, 55, 493-513. 1994.
[10] Saunders Mac Lane, Categories for the Working Mathematician, New York, Springer. 1998.
[11] W. Dzik, J. Järvinen, M. Kondo, M., “Representing Expansions of Bounded Distributive Lattices with Galois Connections in terms of Rough Sets”, ArxiV: 1312.6263 v1. 2013.
[12] D. Schmidt: http://people.cis.ksu.edu/~schmidt/, consultado el 05/08/2014.
[13] Peter Smith, The Galois Connections between Syntax and Semantics, University of Cambridge. 2010
[14] María Manzano, Teoría de Modelos, Alianza, Madrid. 1989.
[15] García-Pardo, et al. On Galois Connections and Soft Computing, Advances in Computational Intelligence, Lecture Notes in Computer Science, vol. 7903, pp. 224-235, Springer, USA, 2013.
[16] E. Orlowska, Z. Pawlak, Representation of non-deterministic Information. Theoretical Computer Science, 55, 493-513. 1984.
[17] J. Järvinen, M. Kondo, J. Kortelainen, “Modal-Like Operators in Boolean Lattices, Galois Connections and Fixed Points”, Fundamenta Informaticae, Vol.76, pp.129-145. 2007.
[18] Y.Y. Yao, “Granular Computing”, Computer Science, Vol. 31, pp. 1-5. 2004.
[19] Hong Li, Xiaoping Ma, Zhenghua Xin, A new formal representation of granules based on features, Computer Modelling & New Technologies, 18(6) 37-43. 2014.
[20] G. Birkhoff, Lattice Theory, third edition, AMS Colloquium, USA. 1967.
[21] Z. Pawlak, “Information Systems Theoretical Foundations”, Information Systems, 6:205-218. 1981.
[22] Burghard von Karger, “Temporal Algebra, Math. Struct”, in Comp. Science, Vol 8, Nº 3, pp. 277-320. 1998.
[23] Lech Polkowski, Andrzej Skowron, Synthesis of Complex Objects: Rough Mereological Approach, ECAI 98, Warsaw University of Technology, Poland. 1998.
[24] Ewa Orlowska, “Logical Aspects of Learning Concepts”, International Journal of Approximate Reasoning, 2:349-364. 1988
[25] Ivo Düntsch, Günter Gediga, “Approximation operators in qualitative data analysis”, Lecture notes in Computer Sciences, vol. 2929, pp. 214-230. 2003
[26] L. A. Zadeh, Fuzzy sets and information granularity, Advances in Fuzzy Set Theory and Applications, pp. 3-18, North Holland, Amsterdam. 1979.
[27] A. Mani, “Algebraic Semantics of Proto-Transitive Rough Sets”, arXiV: 1410.0572v3. 2014
B. Bibliografía:
- G. Cattaneo, D. Ciucci, Algebraic Structures for Rough Sets, Lecture Notes in Computer Science, Transactions on Rough Sets II, vol. 3135, 208-252, Springer, USA. 2005.
- J. Denniston, et al. Formal Contexts, Formal Context Analysis, and Galois Connections, http://arxiv.org/abs/1309.5134v1. 2013.
- Davis Henriques, Galois Connections, Carnegie Mellon University. 2011.
- Joudi Järvinen, Lattice Theory for Rough Sets, en : Transactions on Rough Sets VI, LNCS Vol. 4374, pp. 400-498, Springer, Berlín. 2007.
- J. Järvinen, S. Radeleczki, L. Veres, Rough Sets Determined by Quasiorders, http://arxiv.org/abs/0810.0633v2. 2009.
- S.C. Mu; J. Oliveira, Programming from Galois Connections, Journal of Logic and Algebraic Programming, 81(6):680-704. 2012.
- Zdislaw Pawlak, Rough Sets, International Journal of Computer and Informatic Science , vol. 11, Nº 5, 341-356. 1982.
Recibido: 2017-11-28
Aprobado: 2017-12-20
Datos de edición: Vol.2 - Nro.2 - Art.2
Fecha de edición: 2017-12-28
URL: http://www.reddi.unlam.edu.ar
|
|